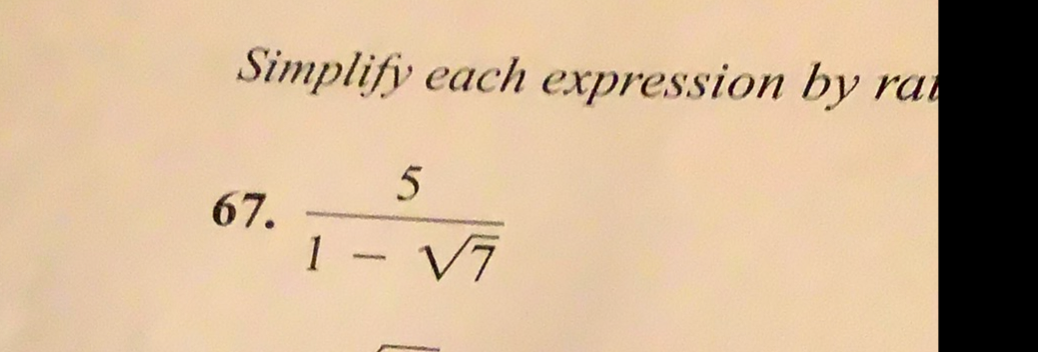Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify each expression (5)/(1-sqrt7)

Simplify each expression.\newline51−7 \frac{5}{1-\sqrt{7}}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Roots of integersright chevron icon

Full solution

Q. Simplify each expression.\newline51−7 \frac{5}{1-\sqrt{7}}
  1. Identify Conjugate of Denominator: Identify the conjugate of the denominator.\newlineThe conjugate of (1−7)(1 - \sqrt{7}) is (1+7)(1 + \sqrt{7}). We will multiply the numerator and the denominator by this conjugate to rationalize the denominator.
  2. Multiply by Conjugate: Multiply the numerator and the denominator by the conjugate. (51−7)⋅1+71+7=5⋅(1+7)(1−7)⋅(1+7)(\frac{5}{1 - \sqrt{7}}) \cdot \frac{1 + \sqrt{7}}{1 + \sqrt{7}} = \frac{5 \cdot (1 + \sqrt{7})}{(1 - \sqrt{7}) \cdot (1 + \sqrt{7})}
  3. Apply Difference of Squares: Apply the difference of squares to the denominator.\newline(1−7)∗(1+7)=12−(7)2=1−7=−6(1 - \sqrt{7}) * (1 + \sqrt{7}) = 1^2 - (\sqrt{7})^2 = 1 - 7 = -6
  4. Distribute Numerator: Distribute the numerator.\newline5×(1+7)=5+5×75 \times (1 + \sqrt{7}) = 5 + 5 \times \sqrt{7}
  5. Combine Results: Combine the results from Step 33 and Step 44.\newline(5+5×7)/(−6)(5 + 5 \times \sqrt{7})/(-6)
  6. Simplify Expression: Simplify the expression by dividing each term in the numerator by the denominator.\newline(5−6)+(5⋅7−6)=−56−(5⋅76)(\frac{5}{-6}) + (\frac{5 \cdot \sqrt{7}}{-6}) = -\frac{5}{6} - (\frac{5 \cdot \sqrt{7}}{6})

More problems from Roots of integers

Question
Find the real-number root. \newline16\sqrt{16}\newline\newlineWrite your answer in simplified form. \newline____\_\_\_\_
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the real-number root. \newline916\sqrt{\frac{9}{16}}\newlineSimplify your answer and write it as a decimal or as a proper or improper fraction.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 3 months ago

Question
Find the real-number root using a calculator. Round your answer to the nearest thousandth. \newline`\sqrt{957} `\newline _______
Get tutor helpright-arrow

Posted 3 months ago

Question
Multiply. Write your answer in simplest form. \newline273×42\sqrt{273} \times \sqrt{42}\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify. \newline634\sqrt{\frac{63}{4}}\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Simplify. Rationalize the denominator.\newline−49−2\frac{-4}{9 - \sqrt{2}}\newline______
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for z z .\newline16=z 16 = \sqrt{z} \newlinez= z = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Simplify the radical expression. 14x14 \sqrt{14x^{14}} Write your answer in the form A A , B \sqrt{B} , or AB A\sqrt{B} , where A A and B B are constants or expressions in x x . Use at most one radical in your answer, and at most one absolute value symbol in your expression for A A . ______
Get tutor helpright-arrow

Posted 3 months ago

Question
Simplify the radical expression.\newline12x12\sqrt{12x^{12}}\newlineWrite your answer in the form AA, B\sqrt{B}, or ABA\sqrt{B}, where AA and BB are constants or expressions in xx. Use at most one radical in your answer, and at most one absolute value symbol in your expression for AA.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 3 months ago

Question
What is the value of sin⁡(5π6)? \sin \left(\frac{5 \pi}{6}\right) ? \newlineChoose 11 answer:\newline(A) −32 -\frac{\sqrt{3}}{2} \newline(B) −22 -\frac{\sqrt{2}}{2} \newline(C) 12 \frac{1}{2} \newline(D) 150150
Get tutor helpright-arrow

Posted 4 months ago

View all (71)