AI tutor
Full solution
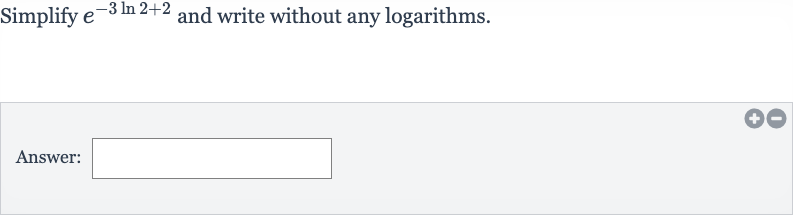
Q. Simplify and write without any logarithms.Answer:
- Apply Power Rule: Apply the power rule of logarithms to the term .The power rule states that , so we can rewrite as .
- Simplify Using Property: Simplify the expression using the property of logarithms. , so we can simplify to .
- Combine Simplified Terms: Combine the simplified term with the remaining part of the exponent.We have , which simplifies to .
- Simplify : Simplify the term . is the same as , which equals .
- Combine Final Answer: Combine the simplified terms to get the final answer.The final expression is .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help