AI tutor
Full solution
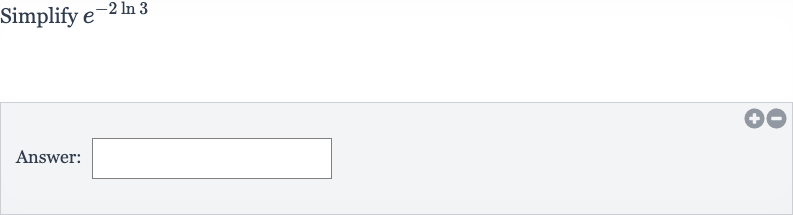
Q. Simplify Answer:
- Recognize Properties: Recognize the properties of logarithms and exponents.We have the expression . The property of logarithms that we can use here is that for any x > 0. We can apply this property in reverse to simplify our expression.
- Apply Power Rule: Apply the power rule for logarithms.The power rule for logarithms states that . We can apply this rule to our expression to simplify it.
- Simplify Using Property: Simplify using the property of and the natural logarithm.Using the property that , we can simplify our expression further.
- Calculate Value: Calculate the value of . means divided by squared.
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help