AI tutor
Full solution
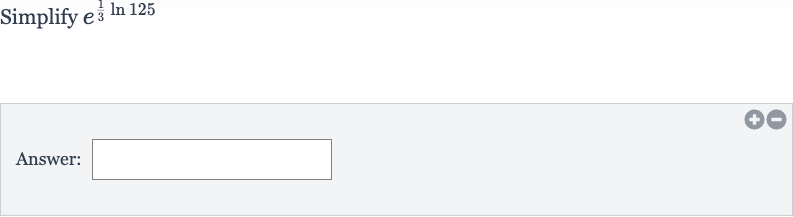
Q. Simplify Answer:
- Identify Base and Exponent: Identify the base and the exponent in .In ,Base: Exponent:
- Use Exponent Property: Use the property of exponents that to simplify the expression.Since is the natural logarithm of , we can rewrite the expression as:
- Simplify Using Property: Simplify the expression using the property from Step .So,
- Calculate Cube Root: Calculate the cube root of . is cubed, so the cube root of is .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help