AI tutor
Full solution
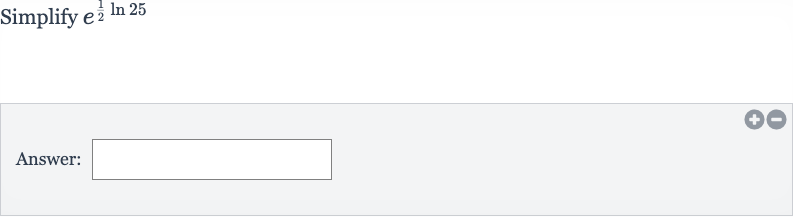
Q. Simplify Answer:
- Recognize Properties: Recognize the properties of logarithms and exponents.The expression can be simplified using the property that . This is because the natural logarithm is the inverse function of the exponential function .
- Apply Exponent: Apply the exponent to the logarithm.Using the property that , we can rewrite the expression as .
- Simplify Expression: Simplify the expression using the property from Step .Since is simply , we now have .
- Calculate Value: Calculate the value of . The expression is equivalent to the square root of , which is .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help