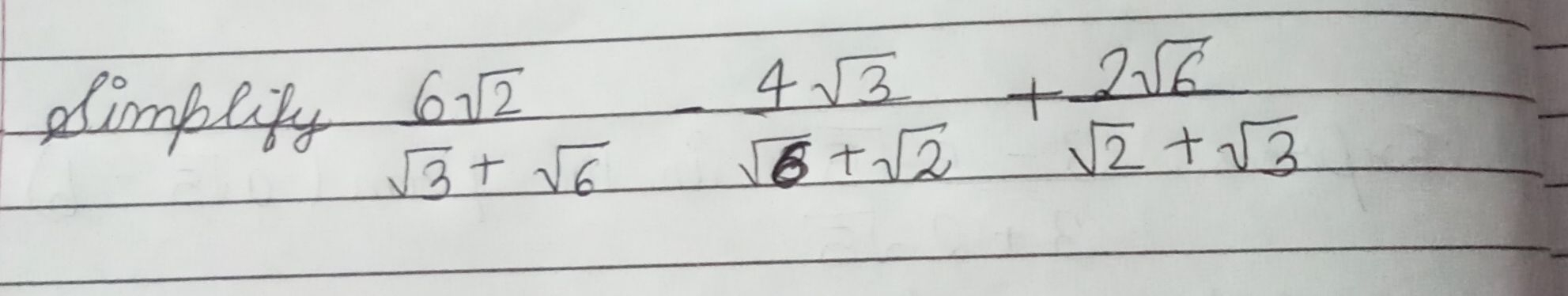Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify (6sqrt2)/(sqrt3+sqrt6)-(4sqrt3)/(sqrt6+sqrt2)+(2sqrt6)/(sqrt2+sqrt3)

Simplify 623+6−436+2+262+3 \frac{6 \sqrt{2}}{\sqrt{3}+\sqrt{6}}-\frac{4 \sqrt{3}}{\sqrt{6}+\sqrt{2}}+\frac{2 \sqrt{6}}{\sqrt{2}+\sqrt{3}}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Simplify rational expressionsright chevron icon

Full solution

Q. Simplify 623+6−436+2+262+3 \frac{6 \sqrt{2}}{\sqrt{3}+\sqrt{6}}-\frac{4 \sqrt{3}}{\sqrt{6}+\sqrt{2}}+\frac{2 \sqrt{6}}{\sqrt{2}+\sqrt{3}}
  1. Rationalize Denominator First Term: Rationalize the denominator of the first term (623+6)(\frac{6\sqrt{2}}{\sqrt{3}+\sqrt{6}}). To do this, multiply the numerator and the denominator by the conjugate of the denominator, which is (3−6)(\sqrt{3}-\sqrt{6}).
  2. Multiply and Simplify First Term: Perform the multiplication for the first term.\newline((62)∗(3−6))/((3+6)∗(3−6))((6\sqrt{2})*(\sqrt{3}-\sqrt{6}))/((\sqrt{3}+\sqrt{6})*(\sqrt{3}-\sqrt{6}))\newlineUse the difference of squares formula a2−b2a^2 - b^2 for the denominator.
  3. Calculate First Term: Calculate the denominator for the first term. \newline(3+6)⋅(3−6)=(3)2−(6)2=3−6=−3(\sqrt{3}+\sqrt{6})\cdot(\sqrt{3}-\sqrt{6}) = (\sqrt{3})^2 - (\sqrt{6})^2 = 3 - 6 = -3
  4. Combine First Term: Calculate the numerator for the first term.\newline(62)⋅(3)−(62)⋅(6)=66−6⋅2=66−12(6\sqrt{2})\cdot(\sqrt{3}) - (6\sqrt{2})\cdot(\sqrt{6}) = 6\sqrt{6} - 6\cdot 2 = 6\sqrt{6} - 12
  5. Rationalize Denominator Second Term: Combine the numerator and the denominator for the first term.\newline(66−12)/(−3)(6\sqrt{6} - 12)/(-3)\newlineDivide each term in the numerator by the denominator.\newline−26+4-2\sqrt{6} + 4
  6. Multiply and Simplify Second Term: Rationalize the denominator of the second term (43)/(6+2)(4\sqrt{3})/(\sqrt{6}+\sqrt{2}). Multiply the numerator and the denominator by the conjugate of the denominator, which is (6−2)(\sqrt{6}-\sqrt{2}).
  7. Calculate Second Term: Perform the multiplication for the second term. (43)(6−2)/((6+2)(6−2))\left(4\sqrt{3}\right)\left(\sqrt{6}-\sqrt{2}\right)/\left(\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{6}-\sqrt{2}\right)\right) Use the difference of squares formula for the denominator.
  8. Combine Second Term: Calculate the denominator for the second term.\newline(6+2)∗(6−2)=(6)2−(2)2=6−2=4(\sqrt{6}+\sqrt{2})*(\sqrt{6}-\sqrt{2}) = (\sqrt{6})^2 - (\sqrt{2})^2 = 6 - 2 = 4
  9. Rationalize Denominator Third Term: Calculate the numerator for the second term.\newline(43)⋅(6)−(43)⋅(2)=4⋅18−4⋅6(4\sqrt{3})\cdot(\sqrt{6}) - (4\sqrt{3})\cdot(\sqrt{2}) = 4\cdot\sqrt{18} - 4\cdot\sqrt{6}\newlineSimplify 18\sqrt{18} to 3⋅23\cdot\sqrt{2}.
  10. Multiply and Simplify Third Term: Continue simplifying the numerator for the second term.\newline4×3×2−4×6=122−464 \times 3 \times \sqrt{2} - 4 \times \sqrt{6} = 12\sqrt{2} - 4\sqrt{6}
  11. Calculate Third Term: Combine the numerator and the denominator for the second term.\newline(122−46)/4(12\sqrt{2} - 4\sqrt{6})/4\newlineDivide each term in the numerator by the denominator.\newline32−63\sqrt{2} - \sqrt{6}
  12. Combine Third Term: Rationalize the denominator of the third term (26)/(2+3)(2\sqrt{6})/(\sqrt{2}+\sqrt{3}). Multiply the numerator and the denominator by the conjugate of the denominator, which is (2−3)(\sqrt{2}-\sqrt{3}).
  13. Combine All Terms: Perform the multiplication for the third term.\newline((26)∗(2−3))/((2+3)∗(2−3))((2\sqrt{6})*(\sqrt{2}-\sqrt{3}))/((\sqrt{2}+\sqrt{3})*(\sqrt{2}-\sqrt{3}))\newlineUse the difference of squares formula for the denominator.
  14. Group and Simplify: Calculate the denominator for the third term. \newline(2+3)∗(2−3)=(2)2−(3)2=2−3=−1(\sqrt{2}+\sqrt{3})*(\sqrt{2}-\sqrt{3}) = (\sqrt{2})^2 - (\sqrt{3})^2 = 2 - 3 = -1
  15. Check and Final Answer: Calculate the numerator for the third term.\newline(26)⋅(2)−(26)⋅(3)=2⋅23−2⋅18(2\sqrt{6})\cdot(\sqrt{2}) - (2\sqrt{6})\cdot(\sqrt{3}) = 2\cdot2\sqrt{3} - 2\cdot\sqrt{18}\newlineSimplify 18\sqrt{18} to 3⋅23\cdot\sqrt{2}.
  16. Check and Final Answer: Calculate the numerator for the third term.\newline(26)⋅(2)−(26)⋅(3)=2⋅23−2⋅18(2\sqrt{6})\cdot(\sqrt{2}) - (2\sqrt{6})\cdot(\sqrt{3}) = 2\cdot2\sqrt{3} - 2\cdot\sqrt{18}\newlineSimplify 18\sqrt{18} to 3⋅23\cdot\sqrt{2}.Continue simplifying the numerator for the third term.\newline43−2⋅3⋅2=43−624\sqrt{3} - 2\cdot3\cdot\sqrt{2} = 4\sqrt{3} - 6\sqrt{2}
  17. Check and Final Answer: Calculate the numerator for the third term.\newline(26)⋅(2)−(26)⋅(3)=2⋅23−2⋅18(2\sqrt{6})\cdot(\sqrt{2}) - (2\sqrt{6})\cdot(\sqrt{3}) = 2\cdot2\sqrt{3} - 2\cdot\sqrt{18}\newlineSimplify 18\sqrt{18} to 3⋅23\cdot\sqrt{2}.Continue simplifying the numerator for the third term.\newline43−2⋅3⋅2=43−624\sqrt{3} - 2\cdot3\cdot\sqrt{2} = 4\sqrt{3} - 6\sqrt{2}Combine the numerator and the denominator for the third term.\newline(43−62)/(−1)(4\sqrt{3} - 6\sqrt{2})/(-1)\newlineMultiply each term in the numerator by the denominator.\newline−43+62-4\sqrt{3} + 6\sqrt{2}
  18. Check and Final Answer: Calculate the numerator for the third term.\newline(26)⋅(2)−(26)⋅(3)=2⋅23−2⋅18(2\sqrt{6})\cdot(\sqrt{2}) - (2\sqrt{6})\cdot(\sqrt{3}) = 2\cdot2\sqrt{3} - 2\cdot\sqrt{18}\newlineSimplify 18\sqrt{18} to 3⋅23\cdot\sqrt{2}.Continue simplifying the numerator for the third term.\newline43−2⋅3⋅2=43−624\sqrt{3} - 2\cdot3\cdot\sqrt{2} = 4\sqrt{3} - 6\sqrt{2}Combine the numerator and the denominator for the third term.\newline(43−62)/(−1)(4\sqrt{3} - 6\sqrt{2})/(-1)\newlineMultiply each term in the numerator by the denominator.\newline−43+62-4\sqrt{3} + 6\sqrt{2}Combine all three terms.\newline(−26+4)−(32−6)+(−43+62)(-2\sqrt{6} + 4) - (3\sqrt{2} - \sqrt{6}) + (-4\sqrt{3} + 6\sqrt{2})
  19. Check and Final Answer: Calculate the numerator for the third term.\newline(26)⋅(2)−(26)⋅(3)=2⋅23−2⋅18(2\sqrt{6})\cdot(\sqrt{2}) - (2\sqrt{6})\cdot(\sqrt{3}) = 2\cdot 2\sqrt{3} - 2\cdot\sqrt{18}\newlineSimplify 18\sqrt{18} to 3⋅23\cdot\sqrt{2}.Continue simplifying the numerator for the third term.\newline43−2⋅3⋅2=43−624\sqrt{3} - 2\cdot 3\cdot\sqrt{2} = 4\sqrt{3} - 6\sqrt{2}Combine the numerator and the denominator for the third term.\newline(43−62)/(−1)(4\sqrt{3} - 6\sqrt{2})/(-1)\newlineMultiply each term in the numerator by the denominator.\newline−43+62-4\sqrt{3} + 6\sqrt{2}Combine all three terms.\newline(−26+4)−(32−6)+(−43+62)(-2\sqrt{6} + 4) - (3\sqrt{2} - \sqrt{6}) + (-4\sqrt{3} + 6\sqrt{2})Group like terms and simplify.\newline(−26−6)+(4+62−32−43)(-2\sqrt{6} - \sqrt{6}) + (4 + 6\sqrt{2} - 3\sqrt{2} - 4\sqrt{3})\newline−36+32−43+4-3\sqrt{6} + 3\sqrt{2} - 4\sqrt{3} + 4
  20. Check and Final Answer: Calculate the numerator for the third term.\newline(26)⋅(2)−(26)⋅(3)=2⋅23−2⋅18(2\sqrt{6})\cdot(\sqrt{2}) - (2\sqrt{6})\cdot(\sqrt{3}) = 2\cdot2\sqrt{3} - 2\cdot\sqrt{18}\newlineSimplify 18\sqrt{18} to 3⋅23\cdot\sqrt{2}.Continue simplifying the numerator for the third term.\newline43−2⋅3⋅2=43−624\sqrt{3} - 2\cdot3\cdot\sqrt{2} = 4\sqrt{3} - 6\sqrt{2}Combine the numerator and the denominator for the third term.\newline(43−62)/(−1)(4\sqrt{3} - 6\sqrt{2})/(-1)\newlineMultiply each term in the numerator by the denominator.\newline−43+62-4\sqrt{3} + 6\sqrt{2}Combine all three terms.\newline(−26+4)−(32−6)+(−43+62)(-2\sqrt{6} + 4) - (3\sqrt{2} - \sqrt{6}) + (-4\sqrt{3} + 6\sqrt{2})Group like terms and simplify.\newline(−26−6)+(4+62−32−43)(-2\sqrt{6} - \sqrt{6}) + (4 + 6\sqrt{2} - 3\sqrt{2} - 4\sqrt{3})\newline−36+32−43+4-3\sqrt{6} + 3\sqrt{2} - 4\sqrt{3} + 4Check for any possible simplifications and write the final answer.\newlineThere are no further simplifications, so the final answer is:\newline−36+32−43+4-3\sqrt{6} + 3\sqrt{2} - 4\sqrt{3} + 4

More problems from Simplify rational expressions

Question
Evaluate the expression for t=−4.4 t = -4.4 .\newlineWrite your answer in simplest form.\newline` frac{t - 4}{t - 2} =` ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. Write your answer using whole numbers and variables.\newlineg3g2−4g\frac{g}{3g^2 - 4g}
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Express your answer as a single fraction in simplest form. 32−5p33\frac{3}{2} - \frac{5p^3}{3} ______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Express your answer as a single fraction in simplest form. \newline1+v5w31 + \frac{v^5w}{3}\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve for h h .\newline−5h−2=−4h−3 \frac{-5}{h - 2} = \frac{-4}{h - 3} \newlineThere may be 11 or 22 solutions.\newlineh= h = _____ or h= h = _____
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the equation of the vertical asymptote of y=1x+9y = \frac{1}{x + 9} ? _____
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the excluded value for y=1x−9−9y = \frac{1}{x - 9} - 9 ?\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Write your answer using whole numbers and variables.\newline9k+49k2+4k\frac{9k + 4}{9k^2 + 4k}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Divide. Write your answer in simplest form.\newlineg−110g3+25g2÷(g−1)\frac{g- 1}{10g^3 + 25g^2} \div (g- 1)\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Express your answer as a single fraction in simplest form. \newline5−3t31\frac{5 - \frac{3}{t^3}}{1}\newline______
Get tutor helpright-arrow

Posted 9 months ago

View all (129)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant