Full solution
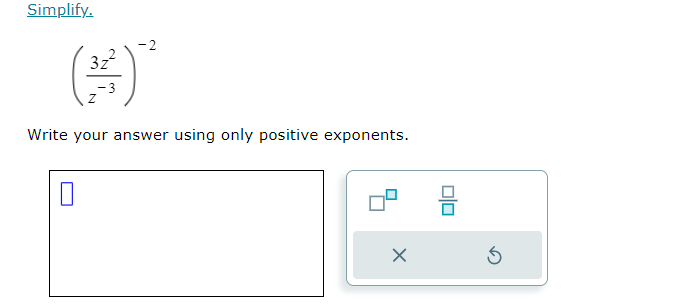
Q. Simplify.Write your answer using only positive exponents.
- Apply Negative Exponent Rule: Apply the negative exponent rule to the entire expression.The negative exponent rule states that . We will apply this rule to the entire expression.
- Simplify Fraction Inside Parentheses: Simplify the expression inside the parentheses before raising it to the power of . We have a fraction raised to a negative exponent. First, we simplify the fraction by applying the rule that .
- Raise Simplified Expression to Power of : Now raise the simplified expression to the power of .We have . When raising a product to an exponent, we raise each factor to the exponent separately.
- Apply Negative Exponent Rule to Original Expression: Apply the negative exponent rule to the original expression with the simplified base.Now we take the reciprocal of the simplified expression from Step , as indicated by the original negative exponent.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help