AI tutor
Full solution
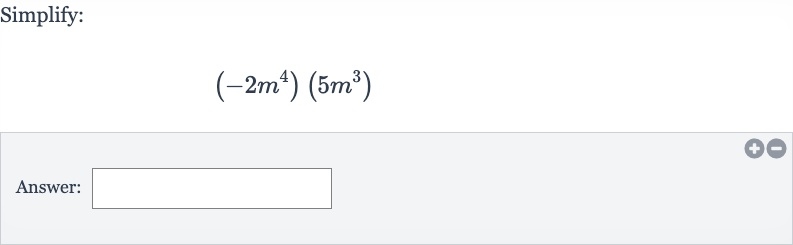
Q. Simplify:Answer:
- Identify Coefficients and Like Terms: Identify the coefficients and the like terms.In the expression , the coefficients are and , and the like terms are and .
- Multiply Coefficients: Multiply the coefficients.Multiply by to get the new coefficient.
- Apply Product Rule for Exponents: Apply the product rule for exponents.When multiplying like bases, add the exponents: .
- Combine Results: Combine the results.Combine the new coefficient from Step with the result from Step to get the final simplified expression.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help