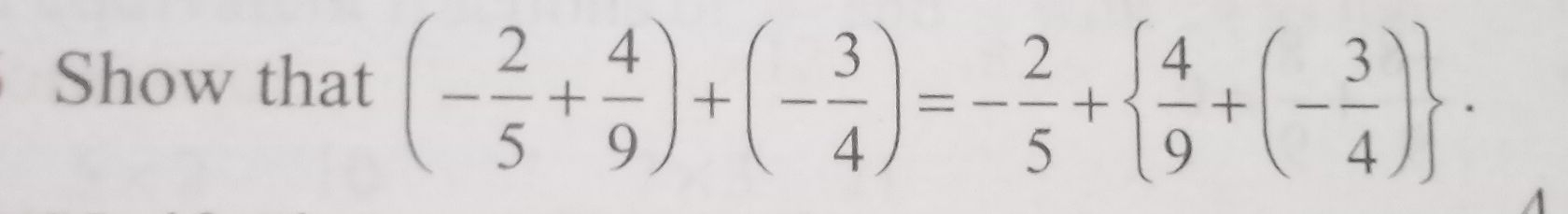Show that (-(2)/(5)+(4)/(9))+(-(3)/(4))=-(2)/(5)+{(4)/(9)+(-(3)/(4))}.

Question

Show that  (-(2)/(5)+(4)/(9))+(-(3)/(4))=-(2)/(5)+{(4)/(9)+(-(3)/(4))}.

Bytelearn · Accepted Answer

Simplify left side: We will start by simplifying the left side of the equation: (-(2)/(5)+(4)/(9))+(-(3)/(4)) First, we add the fractions -(2)/(5) and (4)/(9). Since they have different denominators, we need to find a common denominator.Add fractions with common denominator: The common denominator for 5 and 9 is 45. We convert each fraction to have this common denominator: -(2)/(5) = -(2*9)/(5*9) = -(18)/(45) (4)/(9) = (4*5)/(9*5) = (20)/(45) Now we add these two fractions: -(18)/(45) + (20)/(45) = (20-18)/(45) = (2)/(45)Add remaining fraction: Next, we add the fraction -(3)/(4) to the result (2)/(45). The common denominator for 45 and 4 is 180. We convert each fraction to have this common denominator: (2)/(45) = (2*4)/(45*4) = (8)/(180) -(3)/(4) = -(3*45)/(4*45) = -(135)/(180) Now we add these two fractions: (8)/(180) + (-(135)/(180)) = (8-135)/(180) = -(127)/(180) So the left side of the equation simplifies to: (-(2)/(5)+(4)/(9))+(-(3)/(4)) = -(127)/(180)Simplify right side: Now we simplify the right side of the equation: -(2)/(5)+{(4)/(9)+(-(3)/(4))} We start by adding the fractions (4)/(9) and -(3)/(4). As before, we need a common denominator, which is 36. (4)/(9) = (4*4)/(9*4) = (16)/(36) -(3)/(4) = -(3*9)/(4*9) = -(27)/(36) Now we add these two fractions: (16)/(36) + (-(27)/(36)) = (16-27)/(36) = -(11)/(36)Add fractions with common denominator: We now have the simplified form of the right side of the equation: -(2)/(5)+(-(11)/(36)) The common denominator for 5 and 36 is 180. We convert each fraction to have this common denominator: -(2)/(5) = -(2*36)/(5*36) = -(72)/(180) -(11)/(36) = -(11*5)/(36*5) = -(55)/(180) Now we add these two fractions: -(72)/(180) + (-(55)/(180)) = (-(72+55))/(180) = -(127)/(180) So the right side of the equation simplifies to: -(2)/(5)+{(4)/(9)+(-(3)/(4))} = -(127)/(180)Add remaining fraction: Comparing both sides of the equation, we have: Left side: (-(2)/(5)+(4)/(9))+(-(3)/(4)) = -(127)/(180) Right side: -(2)/(5)+{(4)/(9)+(-(3)/(4))} = -(127)/(180) Since both sides are equal, we have shown that the original equation is true.

Show that $\left(-\frac{2}{5}+\frac{4}{9}\right)+\left(-\frac{3}{4}\right)=-\frac{2}{5}+\left\{\frac{4}{9}+\left(-\frac{3}{4}\right)\right\}$ .

Full solution

More problems from Multiplication with rational exponents

Related topics

Show that (−25+49)+(−34)=−25+{49+(−34)} \left(-\frac{2}{5}+\frac{4}{9}\right)+\left(-\frac{3}{4}\right)=-\frac{2}{5}+\left\{\frac{4}{9}+\left(-\frac{3}{4}\right)\right\} (−52​+94​)+(−43​)=−52​+{94​+(−43​)}.

Show that $\left(-\frac{2}{5}+\frac{4}{9}\right)+\left(-\frac{3}{4}\right)=-\frac{2}{5}+\left\{\frac{4}{9}+\left(-\frac{3}{4}\right)\right\}$ .