Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Show instructions
Question 14 (2 points)
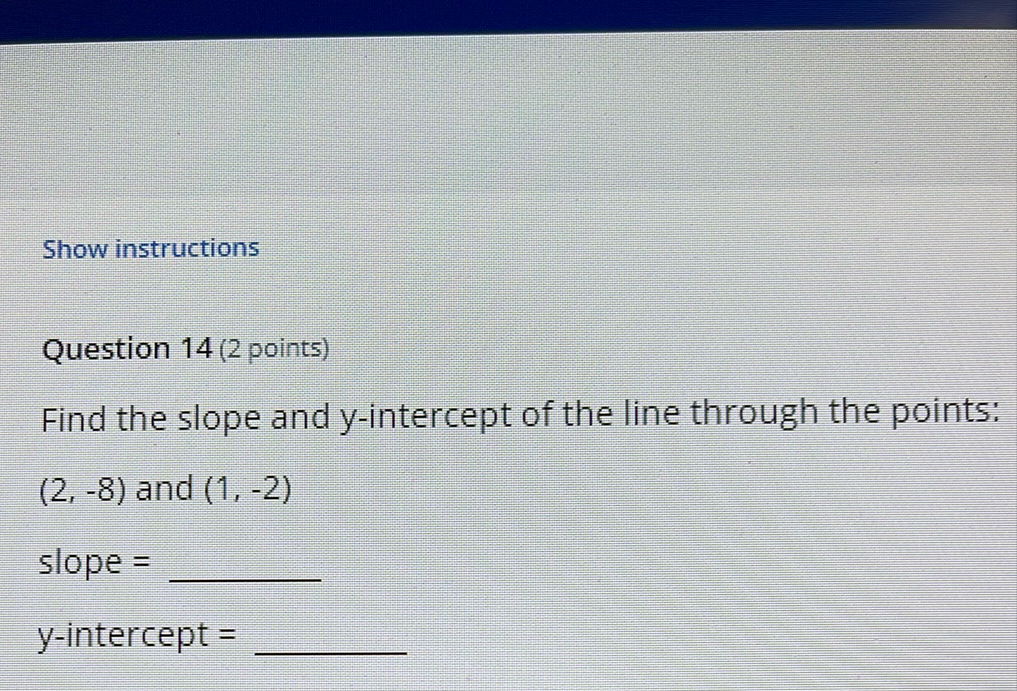
Find the slope and
y-intercept of the line through the points:

(2,-8) and
(1,-2)
slope
=

y-intercept
=

Show instructions $\newline$ Question $14$ ( $2$ points) $\newline$ Find the slope and $y$ -intercept of the line through the points: $\newline$ $(2,-8)$ and $(1,-2)$ $\newline$ slope $=$ $\newline$ $y$ -intercept $=$

View step-by-step help

View step-by-step help

Evaluate variable expressions for sequences

Full solution

Q. Show instructions

\newline

Question

14

(

2

points)

\newline

Find the slope and

y

-intercept of the line through the points:

\newline

(2,-8)

and

(1,-2)

\newline

slope

=

\newline

y

-intercept

=

Calculate Slope: To find the slope $m$ of the line passing through two points $(x_1, y_1)$ and $(x_2, y_2)$ , we use the slope formula: $\newline$ $m = \frac{y_2 - y_1}{x_2 - x_1}$ $\newline$ Let's plug in the values from the points $(2, -8)$ and $(1, -2)$ . $\newline$ $m = \frac{-2 - (-8)}{1 - 2}$
Simplify Slope Calculation: Simplify the calculation for the slope. $\newline$ $m = (-2 + 8) / (1 - 2)$ $\newline$ $m = 6 / -1$ $\newline$ $m = -6$ $\newline$ The slope of the line is $-6$ .
Calculate Y-Intercept: To find the y-intercept $b$ , we can use the slope-intercept form of a line, which is $y = mx + b$ . We can use either of the two points for this calculation. Let's use the point $(2, -8)$ . $\newline$ $-8 = (-6)(2) + b$
Solve for Y-Intercept: Solve for $b$ , the y-intercept. $\newline$ $-8 = -12 + b$ $\newline$ $b = -8 + 12$ $\newline$ $b = 4$ $\newline$ The y-intercept of the line is $4$ .

More problems from Evaluate variable expressions for sequences

Question

Find the sum of the finite arithmetic series.

\sum_{n=1}^{10} (7n+4)

\newline

Posted 2 months ago

Question

Type the missing number in this sequence: `55,\59,\63,\text{_____},\71,\75,\79`

Posted 1 month ago

Question

Type the missing number in this sequence: `2, 4 8`, ______,`32`

Posted 2 months ago

Question

What kind of sequence is this?

2, 10, 50, 250, \ldots

Choices:Choices:

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 2 months ago

Question

What is the missing number in this pattern?

1, 4, 9, 16, 25, 36, 49, 64, 81, \_\_\_\_

Posted 1 month ago

Question

Classify the series.

\sum_{n = 0}^{12} (n + 2)^3

\newline

\newline

\text{[A]arithmetic}

\newline

\text{[B]geometric}

\newline

\text{[C]both}

\newline

\text{[D]neither}

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 6 + 11 + 16 + 21 + 26 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 1 month ago

Question

Find the third partial sum of the series.

\newline

3 + 9 + 15 + 21 + 27 + 33 + \cdots

\newline

Write your answer as an integer or a fraction in simplest form.

\newline

S_3 =

Posted 1 month ago

Question

Find the first three partial sums of the series.

\newline

1 + 7 + 13 + 19 + 25 + 31 + \cdots

\newline

Write your answers as integers or fractions in simplest form.

\newline

S_1 =

\newline

S_2 =

\newline

S_3 =

Posted 2 months ago

Question

Does the infinite geometric series converge or diverge?

\newline

1 + \frac{3}{4} + \frac{9}{16} + \frac{27}{64} + \cdots

\newline

\newline

\text{[A]converge}

\newline

\text{[B]diverge}

Posted 1 month ago