AI tutor
Full solution
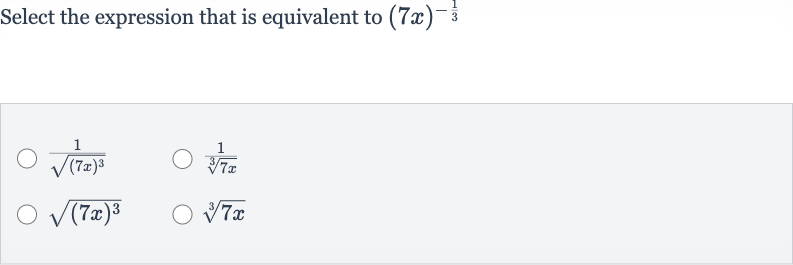
Q. Select the expression that is equivalent to
- Understand Rule for Negative Exponents: Understand the exponent rule for negative exponents. A negative exponent indicates that the base should be taken as the reciprocal. So, means we take the reciprocal of raised to the positive power.
- Apply Negative Exponent Rule: Apply the negative exponent rule. Taking the reciprocal of to the positive power, we get .
- Recognize Meaning of Exponent: Recognize the meaning of the exponent.The exponent corresponds to the cube root. Therefore, is the cube root of .
- Combine Reciprocal and Cube Root: Combine the reciprocal and cube root.The expression is equivalent to taking the cube root of and then taking the reciprocal of that result. This gives us the expression .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help