AI tutor
Full solution
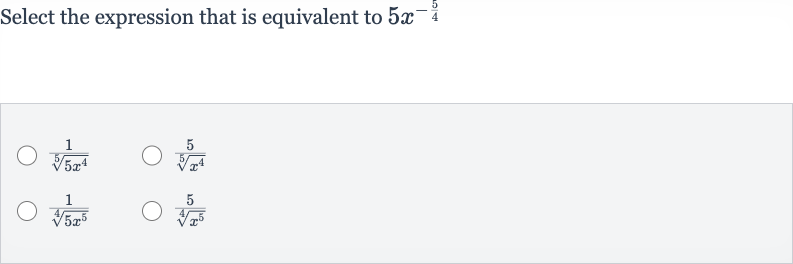
Q. Select the expression that is equivalent to
- Understand Expression: Understand the given expression.The given expression is , which means times raised to the power of negative five-fourths.
- Rewrite Negative Exponent: Rewrite the negative exponent as a reciprocal.A negative exponent means that the base (in this case, ) is on the bottom of a fraction, and the number is multiplied by this fraction.
- Express as Radical: Express as a radical.The exponent means the fourth root of raised to the fifth power.
- Compare with Options: Compare the expression with the given options.We need to find an option that matches the expression . The correct option should have a denominator with the fourth root of to the fifth power.
- Eliminate Incorrect Options: Eliminate incorrect options.Option () has a fifth root and a different exponent, so it's incorrect.Option () has a fifth root, not a fourth root, so it's incorrect.Option () has the correct root but includes inside the root, which is incorrect.Option () matches our expression from Step .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help