AI tutor
Full solution
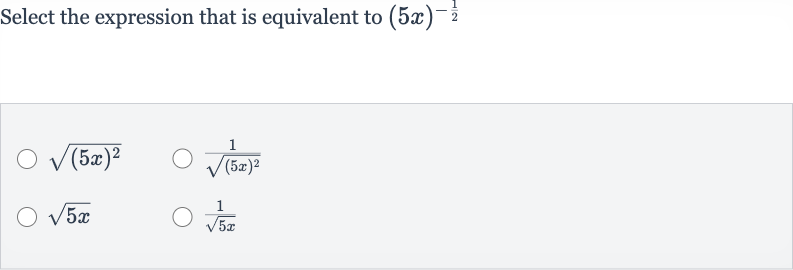
Q. Select the expression that is equivalent to
- Rephrase Question: We need to rephrase the question in one sentence.
- Analyze Given Expression: Let's analyze the given expression . The negative exponent means we take the reciprocal of the base, and the exponent means we take the square root. So, is equivalent to over the square root of .
- Check Options: Now let's check each option to see which one matches our analysis.The first option is . This is not equivalent because it represents the square root of , not the reciprocal of the square root of .
- Option Analysis: The second option is . This option represents the reciprocal of the square root of , which simplifies to , not the reciprocal of the square root of .
- Option Analysis: The third option is . This is not equivalent because it represents the square root of , not the reciprocal of the square root of .
- Option Analysis: The fourth option is . This option represents the reciprocal of the square root of , which matches our analysis of the given expression .
- Option Analysis: Therefore, the expression equivalent to is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help