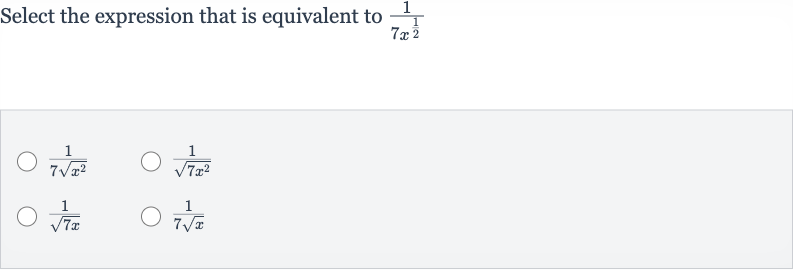AI tutor
Full solution
Q. Select the expression that is equivalent to
- Understand Expression: Understand the given expression.The given expression is . The exponent is equivalent to the square root. Therefore, is the same as .
- Rewrite Using Square Root: Rewrite the given expression using the square root.The expression can be rewritten as .
- Compare with Options: Compare the rewritten expression with the options.The rewritten expression matches one of the given options exactly.
- Eliminate Incorrect Options: Eliminate incorrect options. is incorrect because simplifies to , not . is incorrect because it implies the square root is over both and , which is not the case in the original expression. is incorrect because it implies the square root is over both and , which is not the case in the original expression. is a typographical error and should be written as , which is the correct expression.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help