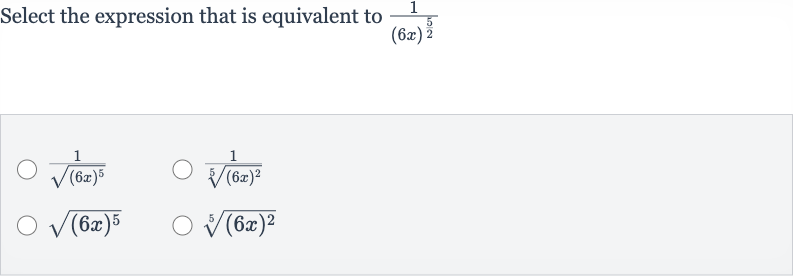Select the expression that is equivalent to (1)/((6x)^((5)/(2))) (1)/(sqrt((6x)^(5))) (1)/(root(5)((6x)^(2))) sqrt((6x)^(5)) root(5)((6x)^(2))

Question

Select the expression that is equivalent to  (1)/((6x)^((5)/(2)))  (1)/(sqrt((6x)^(5)))  (1)/(root(5)((6x)^(2)))  sqrt((6x)^(5))  root(5)((6x)^(2))

Bytelearn · Accepted Answer

Understand Given Expression: Understand the given expression. We are given the expression (1)/((6x)^((5)/(2))) and we need to find an equivalent expression among the options provided.Rewrite Exponent: Rewrite the exponent in the given expression. The exponent (5/2) can be written as a mixed fraction, which is 2 + 1/2, or as 2.5. This means we are looking for the square root of (6x) raised to the 5th power, or (6x) squared raised to the 5/2 power.Analyze Options: Analyze the options. We need to find which option correctly represents the given expression. Let's go through the options one by one.  Option 1: (1)/(sqrt((6x)^(5))) This option represents the square root of (6x) to the 5th power, which is not equivalent to the original expression because the exponent is not correctly represented as 5/2.  Option 2: (1)/(root(5)((6x)^(2))) This option represents the 5th root of (6x) squared, which is not equivalent to the original expression because the exponent is not correctly represented as 5/2.  Option 3: sqrt((6x)^(5)) This option represents the square root of (6x) to the 5th power, which is not equivalent to the original expression because it is not in the form of a reciprocal.  Option 4: root(5)((6x)^(2)) This option represents the 5th root of (6x) squared, which is not equivalent to the original expression because it is not in the form of a reciprocal.  None of the options provided are equivalent to the original expression (1)/((6x)^((5)/(2))).

Select the expression that is equivalent to $\frac{1}{(6 x)^{\frac{5}{2}}}$ $\newline$ $\frac{1}{\sqrt{(6 x)^{5}}}$ $\newline$ $\frac{1}{\sqrt[5]{(6 x)^{2}}}$ $\newline$ $\sqrt{(6 x)^{5}}$ $\newline$ $\sqrt[5]{(6 x)^{2}}$

Full solution

More problems from Multiplication with rational exponents

Related topics

Select the expression that is equivalent to 1(6x)52 \frac{1}{(6 x)^{\frac{5}{2}}} (6x)25​1​\newline1(6x)5 \frac{1}{\sqrt{(6 x)^{5}}} (6x)5​1​\newline1(6x)25 \frac{1}{\sqrt[5]{(6 x)^{2}}} 5(6x)2​1​\newline(6x)5 \sqrt{(6 x)^{5}} (6x)5​\newline(6x)25 \sqrt[5]{(6 x)^{2}} 5(6x)2​

Select the expression that is equivalent to $\frac{1}{(6 x)^{\frac{5}{2}}}$ $\newline$ $\frac{1}{\sqrt{(6 x)^{5}}}$ $\newline$ $\frac{1}{\sqrt[5]{(6 x)^{2}}}$ $\newline$ $\sqrt{(6 x)^{5}}$ $\newline$ $\sqrt[5]{(6 x)^{2}}$