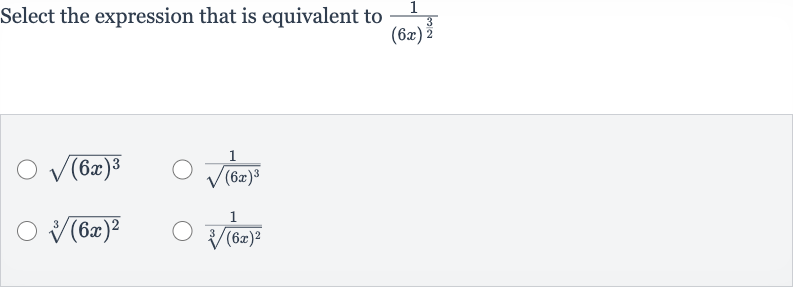
Select the expression that is equivalent to (1)/((6x)^((3)/(2))) sqrt((6x)^(3)) (1)/(sqrt((6x)^(3))) root(3)((6x)^(2)) (1)/(root(3)((6x)^(2)))

Question

Select the expression that is equivalent to  (1)/((6x)^((3)/(2)))  sqrt((6x)^(3))  (1)/(sqrt((6x)^(3)))  root(3)((6x)^(2))  (1)/(root(3)((6x)^(2)))

Bytelearn · Accepted Answer

Understand given expression: We need to find an expression equivalent to (1)/((6x)^((3)/(2))). Let's first understand the given expression. The denominator is (6x) raised to the power of 3/2, which means the square root of (6x) cubed.Rewrite denominator: The square root of a number raised to the third power can be written as the cube of the square root of that number. So, (6x)^(3/2) is equivalent to (sqrt(6x))^3.Replace denominator: Now, we can rewrite the original expression by replacing the denominator with this equivalent form: (1)/((sqrt(6x))^3).Reciprocal of square root: The expression (1)/((sqrt(6x))^3) is the reciprocal of (sqrt(6x))^3. This is equivalent to (1)/(sqrt((6x)^3)) because the cube of the square root of a number is the same as the square root of the cube of that number.Compare with options: We can now compare the rewritten expression with the options given in the new math problem. The expression (1)/(sqrt((6x)^3)) matches the second option: (1)/(sqrt((6x)^(3))).The other options can be quickly checked for correctness. The first option, sqrt((6x)^(3)), is not a reciprocal, so it's not equivalent. The third option, root(3)((6x)^(2)), is a cube root, not a square root, so it's not equivalent. The fourth option, (1)/(root(3)((6x)^(2))), is also not equivalent because it involves a cube root and not the square root of a cube.

Select the expression that is equivalent to $\frac{1}{(6 x)^{\frac{3}{2}}}$ $\newline$ $\sqrt{(6 x)^{3}}$ $\newline$ $\frac{1}{\sqrt{(6 x)^{3}}}$ $\newline$ $\sqrt[3]{(6 x)^{2}}$ $\newline$ $\frac{1}{\sqrt[3]{(6 x)^{2}}}$

Full solution

More problems from Multiplication with rational exponents

Related topics

Select the expression that is equivalent to 1(6x)32 \frac{1}{(6 x)^{\frac{3}{2}}} (6x)23​1​\newline(6x)3 \sqrt{(6 x)^{3}} (6x)3​\newline1(6x)3 \frac{1}{\sqrt{(6 x)^{3}}} (6x)3​1​\newline(6x)23 \sqrt[3]{(6 x)^{2}} 3(6x)2​\newline1(6x)23 \frac{1}{\sqrt[3]{(6 x)^{2}}} 3(6x)2​1​

Select the expression that is equivalent to $\frac{1}{(6 x)^{\frac{3}{2}}}$ $\newline$ $\sqrt{(6 x)^{3}}$ $\newline$ $\frac{1}{\sqrt{(6 x)^{3}}}$ $\newline$ $\sqrt[3]{(6 x)^{2}}$ $\newline$ $\frac{1}{\sqrt[3]{(6 x)^{2}}}$