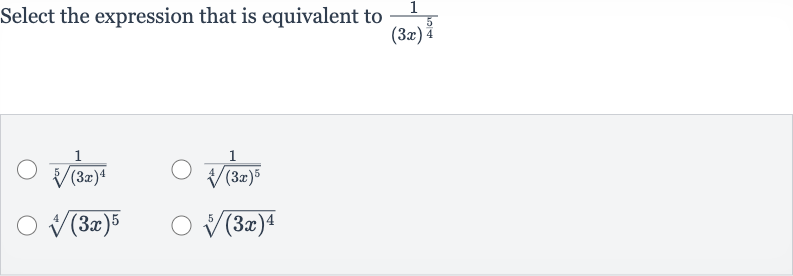AI tutor
Full solution
Q. Select the expression that is equivalent to
- Understand given expression: Understand the given expression.The given expression is . This is a fraction with in the numerator and a power expression in the denominator.
- Rewrite denominator using radical notation: Rewrite the denominator using radical notation.The expression \(3x)^{\frac{}{}}\ can be rewritten using radical notation. The denominator exponent \frac{\(5\)}{\(4\)})\ means the \(4th root of \(3x)\ raised to the th power.
- Apply radical notation: Apply the radical notation to the expression.The expression is equivalent to because the denominator is the th root of to the th power.
- Check other options for equivalence: Check the other options for equivalence.Option is not equivalent because it represents the th root of .Option is not equivalent because it lacks the division by .Option is not equivalent because it represents the th root of .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help