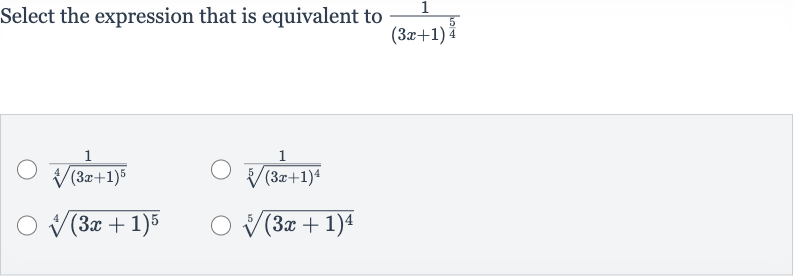Select the expression that is equivalent to (1)/((3x+1)^((5)/(4))) (1)/(root(4)((3x+1)^(5))) (1)/(root(5)((3x+1)^(4))) root(4)((3x+1)^(5)) root(5)((3x+1)^(4))

Question

Select the expression that is equivalent to  (1)/((3x+1)^((5)/(4)))  (1)/(root(4)((3x+1)^(5)))  (1)/(root(5)((3x+1)^(4)))  root(4)((3x+1)^(5))  root(5)((3x+1)^(4))

Bytelearn · Accepted Answer

Interpret Exponent: We are given the expression (1)/((3x+1)^((5)/(4))) and we need to find an equivalent expression among the given options. The exponent (5)/(4) can be interpreted as the 4th root of (3x+1) raised to the 5th power. This is because in fractional exponents, the numerator indicates the power and the denominator indicates the root.Analyze Given Options: Let's analyze the given options to find the equivalent expression. The first option is (1)/(root(4)((3x+1)^(5))). This option correctly represents the 4th root of (3x+1) raised to the 5th power, which is the same as the original expression.Option 1: The second option is (1)/(root(5)((3x+1)^(4))). This option represents the 5th root of (3x+1) raised to the 4th power, which is not equivalent to the original expression because the root and the power are swapped.Option 2: The third option is root(4)((3x+1)^(5)). This option is not equivalent to the original expression because it does not have the fraction (1)/ in front of the root, which means it represents the 4th root of (3x+1) raised to the 5th power without being in the denominator.Option 3: The fourth option is root(5)((3x+1)^(4)). This option is also not equivalent to the original expression for the same reason as the second option; the root and the power are swapped.Option 4: Therefore, the only equivalent expression to the original expression (1)/((3x+1)^((5)/(4))) is the first option: (1)/(root(4)((3x+1)^(5))).

Select the expression that is equivalent to $\frac{1}{(3 x+1)^{\frac{5}{4}}}$ $\newline$ $\frac{1}{\sqrt[4]{(3 x+1)^{5}}}$ $\newline$ $\frac{1}{\sqrt[5]{(3 x+1)^{4}}}$ $\newline$ $\sqrt[4]{(3 x+1)^{5}}$ $\newline$ $\sqrt[5]{(3 x+1)^{4}}$

Full solution

More problems from Multiplication with rational exponents

Related topics