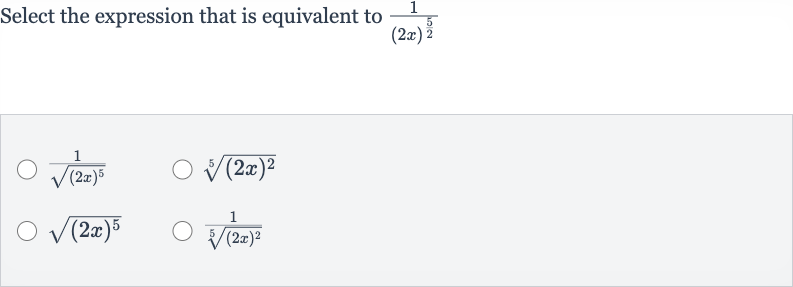Select the expression that is equivalent to (1)/((2x)^((5)/(2))) (1)/(sqrt((2x)^(5))) root(5)((2x)^(2)) sqrt((2x)^(5)) (1)/(root(5)((2x)^(2)))

Question

Select the expression that is equivalent to  (1)/((2x)^((5)/(2)))  (1)/(sqrt((2x)^(5)))  root(5)((2x)^(2))  sqrt((2x)^(5))  (1)/(root(5)((2x)^(2)))

Bytelearn · Accepted Answer

Understand Given Expression: Understand the given expression. The given expression is (1)/((2x)^((5)/(2))). We need to find an equivalent expression among the provided options.Rewrite Using Exponents: Rewrite the given expression using the property of exponents. The exponent (5/2) can be written as a combination of a whole number and a fraction: 2 + 1/2, which corresponds to the square and the square root, respectively. So, (2x)^(5/2) is equivalent to ((2x)^2)^(1/2) * (2x)^(1/2).Simplify Rewritten Expression: Simplify the rewritten expression. ((2x)^2)^(1/2) simplifies to 2x because the square and the square root cancel each other out. The remaining part, (2x)^(1/2), is the square root of 2x. So, (2x)^(5/2) simplifies to 2x * sqrt(2x).Write as Denominator: Write the simplified expression as a denominator. The original expression (1)/((2x)^((5)/(2))) can now be written as 1/(2x * sqrt(2x)).Compare with Provided Options: Compare the simplified expression with the provided options. The correct equivalent expression must have the same base and exponent as our simplified expression. We are looking for an expression that represents the reciprocal of 2x multiplied by the square root of 2x.Eliminate Incorrect Options: Eliminate incorrect options. Option (1)/(sqrt((2x)^(5))) is incorrect because it represents the square root of (2x)^5, not the square root of (2x)^2 multiplied by 2x. Option root(5)((2x)^(2)) is incorrect because it represents the 5th root of (2x)^2, not the reciprocal of 2x multiplied by the square root of 2x. Option sqrt((2x)^(5)) is incorrect because it represents the square root of (2x)^5, not the reciprocal of 2x multiplied by the square root of 2x. Option (1)/(root(5)((2x)^(2))) is the correct equivalent expression because it represents the reciprocal of the 5th root of (2x)^2, which is the same as the original expression (1)/((2x)^((5)/(2))).

Select the expression that is equivalent to $\frac{1}{(2 x)^{\frac{5}{2}}}$ $\newline$ $\frac{1}{\sqrt{(2 x)^{5}}}$ $\newline$ $\sqrt[5]{(2 x)^{2}}$ $\newline$ $\sqrt{(2 x)^{5}}$ $\newline$ $\frac{1}{\sqrt[5]{(2 x)^{2}}}$

Full solution

More problems from Multiplication with rational exponents

Related topics

Select the expression that is equivalent to 1(2x)52 \frac{1}{(2 x)^{\frac{5}{2}}} (2x)25​1​\newline1(2x)5 \frac{1}{\sqrt{(2 x)^{5}}} (2x)5​1​\newline(2x)25 \sqrt[5]{(2 x)^{2}} 5(2x)2​\newline(2x)5 \sqrt{(2 x)^{5}} (2x)5​\newline1(2x)25 \frac{1}{\sqrt[5]{(2 x)^{2}}} 5(2x)2​1​

Select the expression that is equivalent to $\frac{1}{(2 x)^{\frac{5}{2}}}$ $\newline$ $\frac{1}{\sqrt{(2 x)^{5}}}$ $\newline$ $\sqrt[5]{(2 x)^{2}}$ $\newline$ $\sqrt{(2 x)^{5}}$ $\newline$ $\frac{1}{\sqrt[5]{(2 x)^{2}}}$