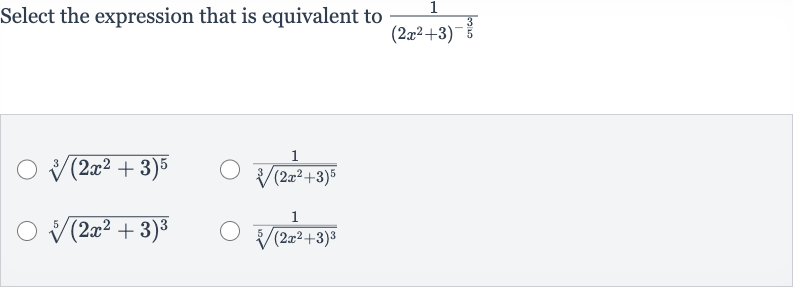AI tutor
Full solution
Q. Select the expression that is equivalent to
- Use Negative Exponent Property: We are given the expression . To simplify this expression, we can use the property of negative exponents which states that .
- Apply Negative Exponent Property: Applying the negative exponent property to our expression, we get:
- Simplify to Positive Exponent: Now we need to find the equivalent expression among the given options. We have simplified the original expression to , which is a positive exponent form. We need to match this with one of the options.
- Find Equivalent Expression: Looking at the options, we can see that the equivalent expression in radical form would be the fifth root of raised to the third power, because the exponent means the fifth root (denominator) of the quantity raised to the third power (numerator).
- Convert to Radical Form: The correct expression in radical form is therefore:
- Match with Given Options: Comparing this with the given options, we find that the equivalent expression is:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help