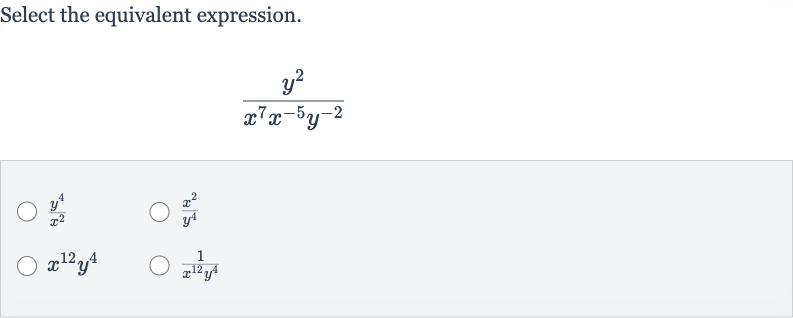AI tutor
Full solution
Q. Select the equivalent expression.
- Combine Exponents Like Bases: Simplify the expression by combining the exponents of like bases using the properties of exponents.For the base , we have , which simplifies to because when you multiply with the same base, you add the exponents.For the base , we have , which simplifies to because when you multiply with the same base, you add the exponents.
- Calculate Exponents: Perform the calculations for the exponents.For the base , we have which equals .For the base , we have which equals .
- Remember Power of : Remember that any number raised to the power of is . So, equals .
- Combine Simplified Terms: Combine the simplified terms.Since equals , it does not affect the expression when multiplied.The simplified expression is , which is just .
- Compare with Options: Compare the simplified expression with the given options. The equivalent expression is , which is not the same as our simplified expression .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help