AI tutor
Full solution
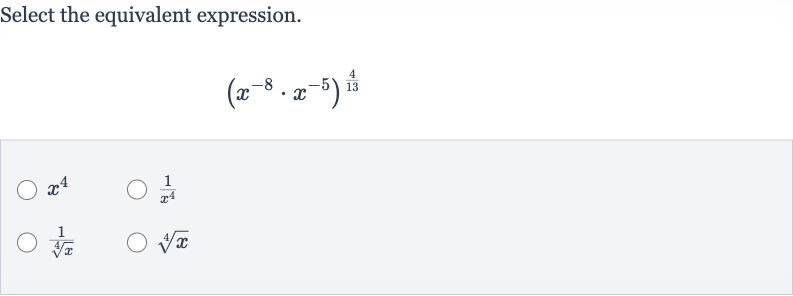
Q. Select the equivalent expression.
- Apply Exponent Rule: Apply the exponent rule for multiplying powers with the same base.When multiplying powers with the same base, we add the exponents.
- Apply Power of Power Rule: Apply the power of a power rule.When raising a power to another power, we multiply the exponents.
- Rewrite with Positive Exponent: Rewrite the expression with a positive exponent. is equivalent to .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help