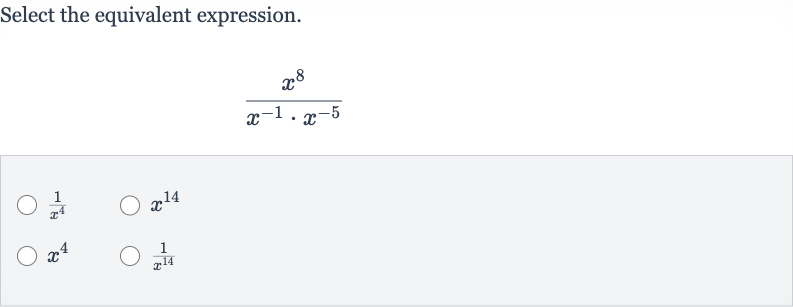AI tutor
Full solution
Q. Select the equivalent expression.
- Simplify Exponents: Simplify the denominator using the property of exponents that states when you multiply powers with the same base, you add the exponents.
- Rewrite Expression: Rewrite the original expression with the simplified denominator. becomes
- Apply Exponent Rule: Use the property of exponents that states when you divide powers with the same base, you subtract the exponents.= =
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help