AI tutor
Full solution
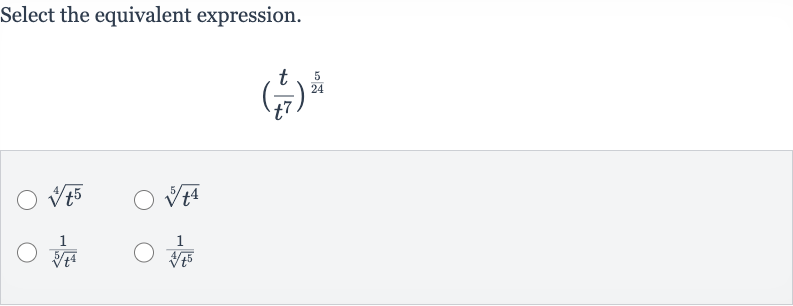
Q. Select the equivalent expression.
- Simplify Base: Simplify the base of the given expression.We have . First, we simplify the fraction inside the parentheses by using the property of exponents that states when dividing like bases, we subtract the exponents.
- Apply Exponent: Apply the exponent to the simplified base.Now we have . We use the property of exponents that states to simplify the expression..
- Convert Negative Exponent: Convert the negative exponent to a positive exponent by taking the reciprocal. can be rewritten as . This is because a negative exponent indicates the reciprocal of the base raised to the positive of that exponent.
- Rewrite as Radical: Rewrite the expression as a radical. can be rewritten as a radical expression. The denominator of the exponent () becomes the index of the root, and the numerator () becomes the exponent inside the root..
- Compare with Options: Compare the result with the given options.The expression we have found, , matches one of the given options.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help