AI tutor
Full solution
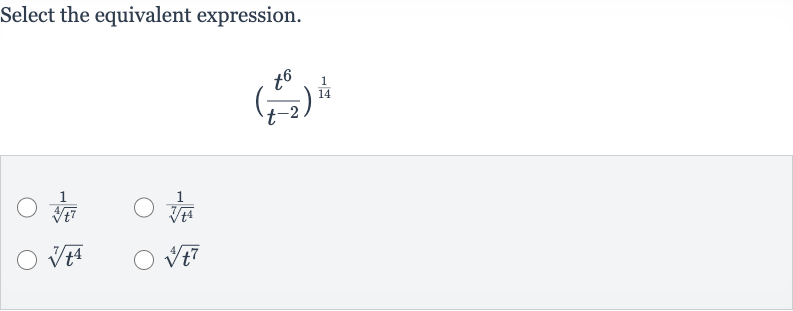
Q. Select the equivalent expression.
- Simplify Exponents in Parentheses: Simplify the expression inside the parentheses by adding the exponents of . When dividing powers with the same base, subtract the exponents: . So,
- Apply Exponent Rule: Apply the exponent to the simplified base . Now we have . When raising a power to a power, multiply the exponents: . So, .
- Convert to Radical Expression: Convert the exponent to a radical expression.The expression can be written as the th root of raised to the th power, which is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help