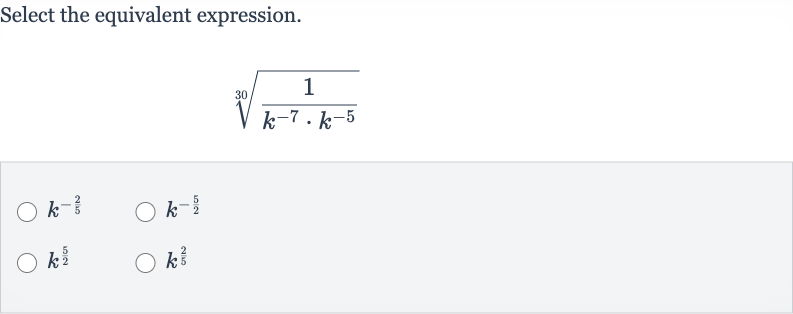AI tutor
Full solution
Q. Select the equivalent expression.
- Simplify Inside Radical: We are given the expression:First, we need to simplify the expression inside the radical.
- Combine Exponents: Since the bases are the same , we can add the exponents when multiplying: So, the expression becomes:
- Move to Numerator: Now, we can rewrite the expression by moving to the numerator and changing the sign of the exponent:
- Rewrite Radical as Exponent: The radical can be rewritten as an exponent of :
- Multiply Exponents: When raising a power to a power, we multiply the exponents: k^{\(12\)})^{\frac{\(1\)}{\(30\)}} = k^{\(12\) \times \frac{\(1\)}{\(30\)}} = k^{\frac{\(12\)}{\(30\)}}\
- Simplify Fraction: We can simplify the fraction \(\frac{12}{30} by dividing both the numerator and the denominator by their greatest common divisor, which is :
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help