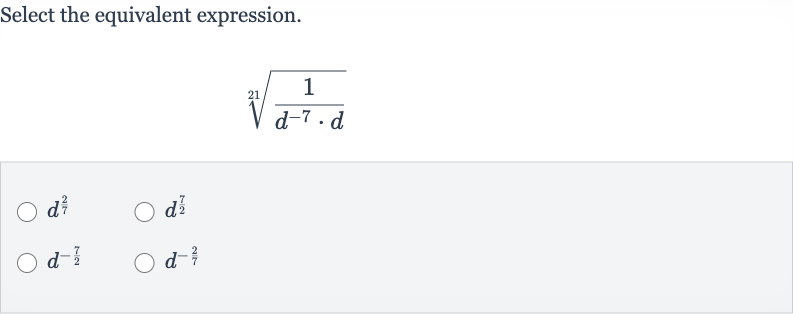AI tutor
Full solution
Q. Select the equivalent expression.
- Simplify Inside Radical: Simplify the expression inside the radical.We have the expression . First, we need to simplify the denominator by multiplying by .Using the property of exponents that states , we get:.So, the expression becomes .
- Move Denominator to Numerator: Simplify the expression further by moving the denominator to the numerator.Using the property of exponents that states , we can rewrite the expression as:.
- Convert to Exponent Form: Convert the radical expression to an exponent form.The root of can be written as .Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is ..
- Identify Equivalent Expression: Identify the equivalent expression from the given options.The simplified expression is , which matches one of the given options.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help