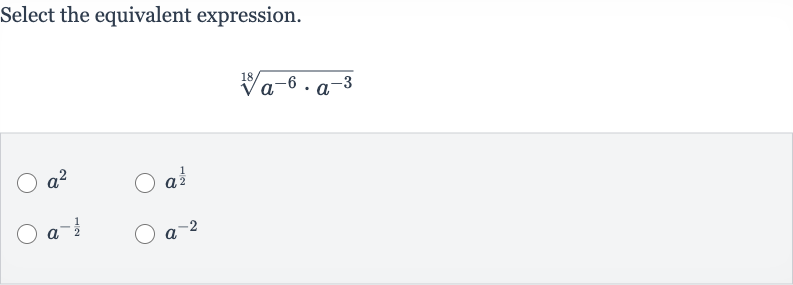AI tutor
Full solution
Q. Select the equivalent expression.
- Understand the problem: Understand the problem.We need to simplify the expression and select the equivalent expression from the given options.
- Apply exponent property: Apply the property of exponents for multiplication.When multiplying two exponents with the same base, we add the exponents.
- Perform exponent addition: Perform the addition of exponents.
- Apply root to exponent: Apply the root to the exponent.The th root of can be written as .
- Simplify exponent fraction: Simplify the fraction in the exponent. simplifies to .
- Match with given options: Match the simplified expression with the given options.The equivalent expression is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help