AI tutor
Full solution
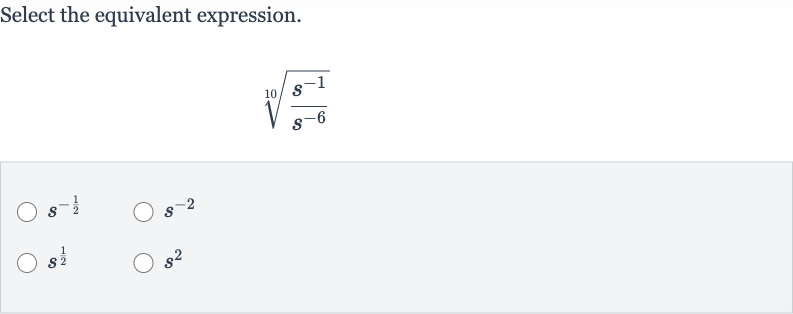
Q. Select the equivalent expression.
- Understand the expression: Understand the given expression.We are given the expression and we need to simplify it to find the equivalent expression.
- Simplify inside the root: Simplify the expression inside the root.The expression inside the root is . When dividing exponential expressions with the same base, we subtract the exponents.So, .
- Apply the root: Apply the root to the simplified expression.Now we have . The root of can be written as .
- Use power of a power rule: Use the power of a power rule.Using the power of a power rule, we multiply the exponents: .
- Identify equivalent expression: Identify the equivalent expression.The equivalent expression is , which is one of the options given.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help