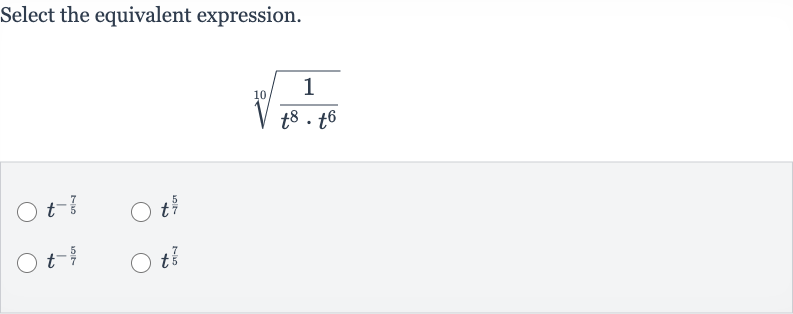AI tutor
Full solution
Q. Select the equivalent expression.
- Understand given expression: We are given the expression:First, we need to understand that the th root of a number can be written as a fractional exponent with the denominator being .So, we can rewrite the expression as:
- Apply exponent rule: Next, we apply the exponent rule for multiplying with the same base, which states that when we multiply two exponents with the same base, we add the exponents:So, the expression becomes:
- Apply power of a quotient rule: Now, we apply the power of a quotient rule, which states that . In this case, we have:Since raised to any power is , the numerator remains :
- Simplify the exponent: We simplify the exponent by dividing by : So, the expression simplifies to:
- Write with negative exponent: Finally, we can write the expression with a negative exponent to move the term to the numerator: This matches one of the answer choices.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help