AI tutor
Full solution
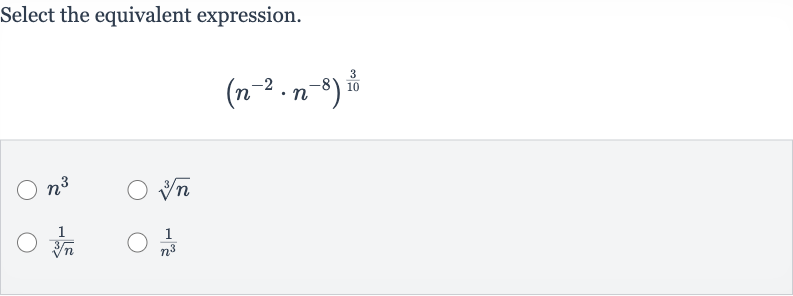
Q. Select the equivalent expression.
- Simplify base with exponents: Simplify the base by adding the exponents.When multiplying two powers with the same base, you add the exponents.
- Apply outer exponent: Apply the outer exponent to the simplified base.Now we have . When raising a power to a power, you multiply the exponents.=
- Rewrite negative exponent: Rewrite the negative exponent as a reciprocal.A negative exponent means that the base is on the wrong side of the fraction line, so you flip it to make the exponent positive.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help