AI tutor
Full solution
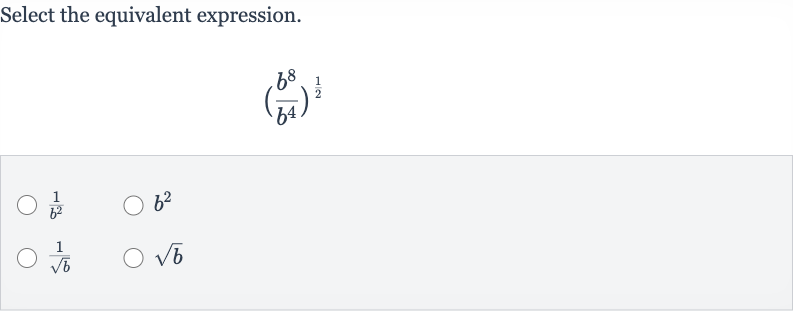
Q. Select the equivalent expression.
- Simplify Exponents: Simplify the expression inside the parentheses using the properties of exponents.When dividing like bases with exponents, subtract the exponents.
- Apply Exponent Rule: Apply the exponent outside the parentheses to the result from Step . means taking the square root of .The square root of is .
- Check Final Result: Check the final result against the given options.The equivalent expression is .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help