Full solution
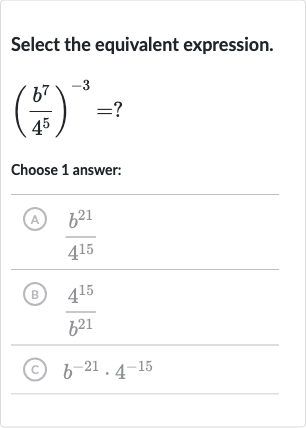
Q. Select the equivalent expression.?Choose answer:(A) (B) (C)
- Understand Exponent Properties: First, we need to understand the properties of exponents. When an expression in the form of is given, it can be rewritten as . In this case, our expression is . We will apply this property to simplify the expression.
- Apply Exponent Rule: Applying the exponent rule, we get:This means we raise both the numerator and the denominator to the power of .
- Simplify Using Power Rule: Simplify the expression further by applying the power of a power rule, which states that . Therefore, we have:This simplifies to:
- Handle Negative Exponents: Now, we need to understand what it means to have a negative exponent. The rule for negative exponents states that . Applying this rule to both the numerator and the denominator, we get:This simplifies to:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help