Full solution
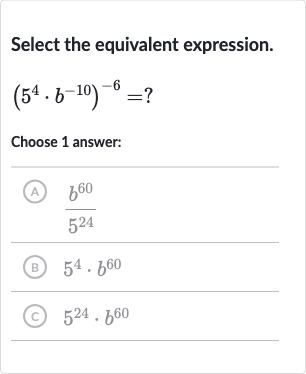
Q. Select the equivalent expression.Choose answer:(A) (B) (C)
- Apply Power Rule: Apply the power of a power rule.The power of a power rule states that . We will apply this rule to both and separately.
- Multiply Exponents: Multiply the exponents.Now we multiply the exponents for each base.
- Combine Results: Combine the results.We now have two separate terms, and . We combine them to form the final expression.
- Simplify with Negative Exponent: Simplify the expression with negative exponent.The term can be rewritten as because a negative exponent indicates the reciprocal of the base raised to the positive exponent.
- Rearrange Expression: Rearrange the expression.We can rearrange the expression to match the answer choices. * =
- Match with Answer Choices: Match the expression with the answer choices.The expression matches answer choice .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help