Full solution
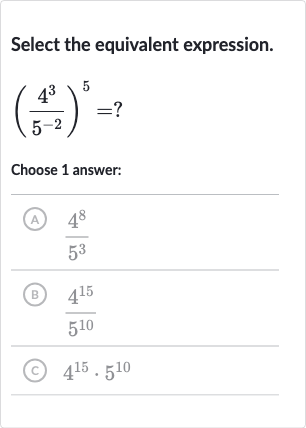
Q. Select the equivalent expression.?Choose answer:(A) (B) (C)
- Apply power rule: Apply the power of a power rule.The power of a power rule states that . We will apply this rule to both the numerator and the denominator separately.
- Calculate exponents: Calculate the exponents.Now we will multiply the exponents.
- Simplify with negative exponent: Simplify the expression with negative exponent.A negative exponent means that the base is on the wrong side of the fraction line, so you flip the base to the other side. Therefore, becomes .
- Write final expression: Write the final expression.The final expression is , which corresponds to one of the answer choices.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help