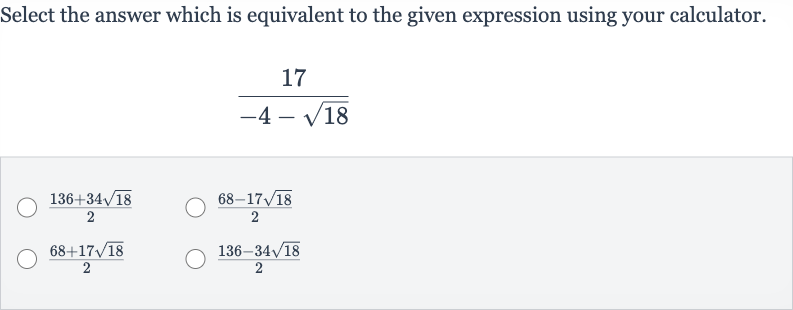Select the answer which is equivalent to the given expression using your calculator. (17)/(-4-sqrt18) (136+34sqrt18)/(2) (68-17sqrt18)/(2) (68+17sqrt18)/(2) (136-34sqrt18)/(2)

Question

Select the answer which is equivalent to the given expression using your calculator.  (17)/(-4-sqrt18)  (136+34sqrt18)/(2)  (68-17sqrt18)/(2)  (68+17sqrt18)/(2)  (136-34sqrt18)/(2)

Bytelearn · Accepted Answer

Simplify Denominator: Simplify the denominator of the given expression. We have the expression (17)/(-4-sqrt18). To simplify, we first need to rationalize the denominator. Rationalizing the denominator involves multiplying the numerator and the denominator by the conjugate of the denominator. The conjugate of -4-sqrt18 is -4+sqrt18.Multiply by Conjugate: Multiply the numerator and the denominator by the conjugate of the denominator. We multiply (17)/(-4-sqrt18) by (-4+sqrt18)/(-4+sqrt18) to rationalize the denominator. (17 * (-4+sqrt18)) / ((-4-sqrt18) * (-4+sqrt18))Apply Difference of Squares: Apply the difference of squares to the denominator. (-4-sqrt18) * (-4+sqrt18) simplifies to (-4)^2 - (sqrt18)^2, which is 16 - 18. 16 - 18 = -2.Distribute Numerator: Distribute the numerator. Now we distribute 17 to both terms in the conjugate (-4+sqrt18). 17 * (-4) + 17 * sqrt18 = -68 + 17sqrt18.Combine Results: Combine the results to get the simplified expression. We now have (-68 + 17sqrt18) / -2. To simplify further, we divide both terms in the numerator by -2. (-68 / -2) + (17sqrt18 / -2) = 34 - (17sqrt18 / 2).Check Answer Choices: Check the answer choices. We need to find the answer choice that matches our simplified expression 34 - (17sqrt18 / 2). The correct answer choice is (68 - 17sqrt18) / 2, which simplifies to 34 - (17sqrt18 / 2) when each term in the numerator is divided by 2.

Select the answer which is equivalent to the given expression using your calculator. $\newline$ $\frac{17}{-4-\sqrt{18}}$ $\newline$ $\frac{136+34 \sqrt{18}}{2}$ $\newline$ $\frac{68-17 \sqrt{18}}{2}$ $\newline$ $\frac{68+17 \sqrt{18}}{2}$ $\newline$ $\frac{136-34 \sqrt{18}}{2}$

Full solution

More problems from Multiplication with rational exponents

Related topics