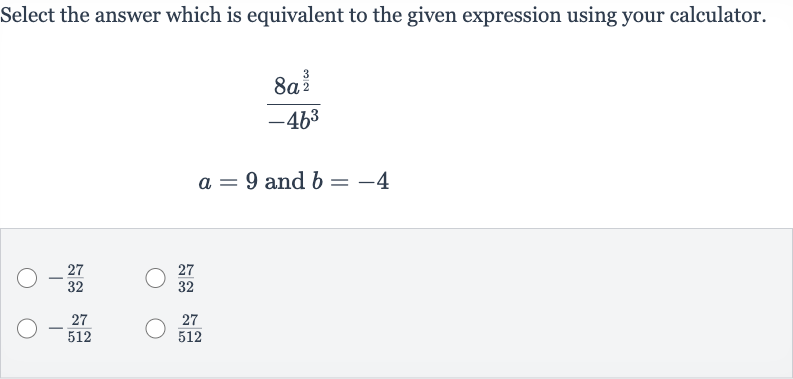Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Select the answer which is equivalent to the given expression using your calculator.

(8a^((3)/(2)))/(-4b^(3))

a=9" and "b=-4

-(27)/(32)

(27)/(32)

-(27)/(512)

(27)/(512)

Select the answer which is equivalent to the given expression using your calculator. $\newline$ $\frac{8 a^{\frac{3}{2}}}{-4 b^{3}}$ $\newline$ $a=9 \text { and } b=-4$ $\newline$ $-\frac{27}{32}$ $\newline$ $\frac{27}{32}$ $\newline$ $-\frac{27}{512}$ $\newline$ $\frac{27}{512}$

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Select the answer which is equivalent to the given expression using your calculator.

\newline

\frac{8 a^{\frac{3}{2}}}{-4 b^{3}}

\newline

a=9 \text { and } b=-4

\newline

-\frac{27}{32}

\newline

\frac{27}{32}

\newline

-\frac{27}{512}

\newline

\frac{27}{512}

Substitute Values: Substitute the given values of $a$ and $b$ into the expression. $\newline$ We have the expression $\frac{8a^{\frac{3}{2}}}{-4b^3}$ and we are given that $a=9$ and $b=-4$ . Let's substitute these values into the expression. $\newline$ $\frac{8 \times 9^{\frac{3}{2}}}{-4 \times (-4)^3}$
Simplify Exponent for a: Simplify the exponent for a. $9^{\frac{3}{2}}$ means the square root of $9$ raised to the $3$ rd power. The square root of $9$ is $3$ , so we have: $(8 \times (3^3)) / (-4 \times (-4)^3)$
Calculate Value of $3^3$ : Calculate the value of $3^3$ . $3^3$ is $3$ multiplied by itself three times, which is $27$ . $(8 \times 27) / (-4 \times (-4)^3)$
Simplify Exponent for $b$ : Simplify the exponent for $b$ . $(-4)^3$ means $-4$ multiplied by itself three times, which is $-64$ . $\frac{8 \times 27}{-4 \times -64}$
Multiply Numerators and Denominators: Multiply the numerators and denominators. $\newline$ Now we multiply $8$ by $27$ and $-4$ by $-64$ . $\newline$ $(216) / (256)$
Simplify Fraction: Simplify the fraction. $\newline$ Both $216$ and $256$ are divisible by $8$ . Let's divide both by $8$ to simplify the fraction. $\newline$ $(216/8) / (256/8)$ $\newline$ $(27) / (32)$
Determine Sign: Determine the sign of the result. $\newline$ Since we divided a negative by a negative in the denominator, the result is positive. $\newline$ The final answer is $(27)/(32)$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant