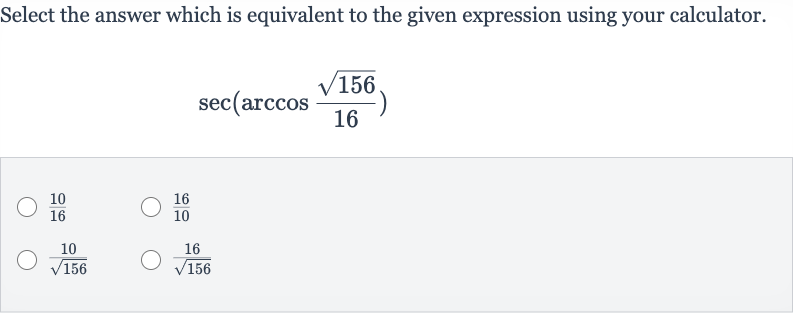Full solution
Q. Select the answer which is equivalent to the given expression using your calculator.
- Understand secant function: First, let's understand the expression . The secant function is the reciprocal of the cosine function. So, . Therefore, , because is the angle whose cosine is .
- Apply understanding to expression: Now, let's apply this understanding to our expression. To simplify this, we can multiply the numerator and the denominator by .
- Simplify expression: After multiplying by , we get:This is one of the options given, so we can conclude that this is the equivalent expression.