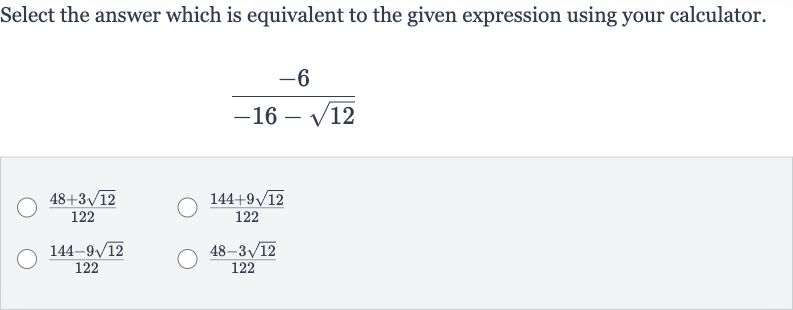Select the answer which is equivalent to the given expression using your calculator. (-6)/(-16-sqrt12) (48+3sqrt12)/(122) (144+9sqrt12)/(122) (144-9sqrt12)/(122) (48-3sqrt12)/(122)

Question

Select the answer which is equivalent to the given expression using your calculator.  (-6)/(-16-sqrt12)  (48+3sqrt12)/(122)  (144+9sqrt12)/(122)  (144-9sqrt12)/(122)  (48-3sqrt12)/(122)

Bytelearn · Accepted Answer

Simplify square root: First, simplify the square root in the denominator of the given expression. √12 = √(4*3) = √4 * √3 = 2√3Substitute simplified value: Now, substitute the simplified square root back into the original expression. (-6)/(-16-2√3)Multiply by conjugate: To eliminate the square root from the denominator, multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of (-16-2√3) is (-16+2√3). ((-6)/(-16-2√3)) * ((-16+2√3)/(-16+2√3)) = ((-6)*(-16+2√3))/((-16-2√3)*(-16+2√3))Perform numerator multiplication: Perform the multiplication in the numerator. (-6)*(-16+2√3) = 96 - 12√3Use difference of squares: Perform the multiplication in the denominator using the difference of squares formula. ((-16)^2 - (2√3)^2) = 256 - 4*3 = 256 - 12 = 244Write simplified expression: Now, write the simplified expression with the multiplied numerator and denominator. (96 - 12√3) / 244Divide by greatest common divisor: To simplify further, divide both terms in the numerator by the denominator. 96/244 - (12√3)/244Perform division: Simplify the fractions by dividing the numerator and denominator by their greatest common divisor, which is 4 for the first term and 12 for the second term. (96/4) / (244/4) - (12/12)√3 / (244/12)Correct second term division: Perform the division for both terms. 24/61 - √3/20.3333...Since the denominator 20.3333... is not a simplified fraction, we need to correct this. The correct division for the second term is (12√3)/244 = (√3)/20.3333... = (√3)/20.3333... = √3/20.3333...

Select the answer which is equivalent to the given expression using your calculator. $\newline$ $\frac{-6}{-16-\sqrt{12}}$ $\newline$ $\frac{48+3 \sqrt{12}}{122}$ $\newline$ $\frac{144+9 \sqrt{12}}{122}$ $\newline$ $\frac{144-9 \sqrt{12}}{122}$ $\newline$ $\frac{48-3 \sqrt{12}}{122}$

Full solution

More problems from Sum of finite series starts from 1

Related topics