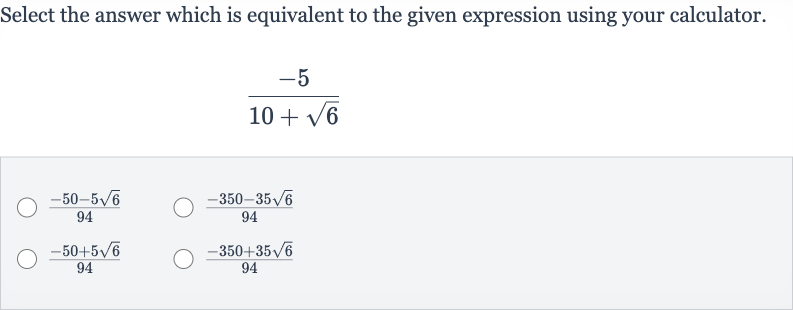Full solution
Q. Select the answer which is equivalent to the given expression using your calculator.
- Rationalize Denominator: To find the equivalent expression, we need to rationalize the denominator of the given expression . This means we need to eliminate the square root from the denominator.
- Multiply by Conjugate: To rationalize the denominator, we multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of is .
- Simplify Numerator: Now, multiply the numerator and the denominator by the conjugate:
- Simplify Denominator: Simplify the numerator: .
- Final Simplified Expression: Simplify the denominator using the difference of squares formula: .
- Compare with Answer Choices: Now we have the simplified expression: .
- Compare with Answer Choices: Now we have the simplified expression: .Comparing the simplified expression with the answer choices, we find that the equivalent expression is .