Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

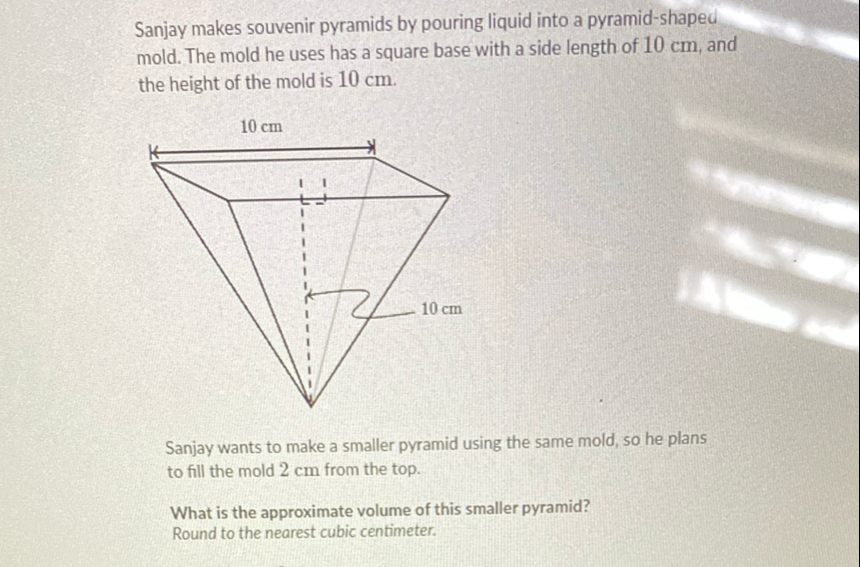
Sanjay makes souvenir pyramids by pouring liquid into a pyramid-shaped mold. The mold he uses has a square base with a side length of 10cm, and the height of the mold is 10cm. Sanjay wants to make a smaller pyramid using the same mold, so he plans to fill the mold 2cm from the top. What is the approximate volume of this smaller pyramid? Round to the nearest cubic centimeter.

Sanjay makes souvenir pyramids by pouring liquid into a pyramid-shaped mold. The mold he uses has a square base with a side length of 10 cm 10 \mathrm{~cm} , and the height of the mold is 10 cm 10 \mathrm{~cm} .\newlineSanjay wants to make a smaller pyramid using the same mold, so he plans to fill the mold 2 cm 2 \mathrm{~cm} from the top.\newlineWhat is the approximate volume of this smaller pyramid?\newlineRound to the nearest cubic centimeter.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Pythagorean Theorem and its converseright chevron icon

Full solution

Q. Sanjay makes souvenir pyramids by pouring liquid into a pyramid-shaped mold. The mold he uses has a square base with a side length of 10 cm 10 \mathrm{~cm} , and the height of the mold is 10 cm 10 \mathrm{~cm} .\newlineSanjay wants to make a smaller pyramid using the same mold, so he plans to fill the mold 2 cm 2 \mathrm{~cm} from the top.\newlineWhat is the approximate volume of this smaller pyramid?\newlineRound to the nearest cubic centimeter.
  1. Understand Problem & Formula: Understand the problem and the formula for the volume of a pyramid. The volume of a pyramid is given by the formula V=(13)×base area×heightV = (\frac{1}{3}) \times \text{base area} \times \text{height}. Since the base is square, the base area is the side length squared.
  2. Calculate Full-Size Pyramid: Calculate the volume of the full-size pyramid using the given dimensions.\newlineThe side length of the base ss is 10 cm10\,\text{cm}, and the height hh is also 10 cm10\,\text{cm}.\newlineUsing the formula V=13×s2×hV = \frac{1}{3} \times s^2 \times h, we get V=13×10 cm×10 cm×10 cmV = \frac{1}{3} \times 10\,\text{cm} \times 10\,\text{cm} \times 10\,\text{cm}.
  3. Perform Calculation: Perform the calculation for the full-size pyramid. V=13×10 cm×10 cm×10 cm=13×1000 cm3=333.33 cm3V = \frac{1}{3} \times 10\,\text{cm} \times 10\,\text{cm} \times 10\,\text{cm} = \frac{1}{3} \times 1000\,\text{cm}^3 = 333.33\,\text{cm}^3 (rounded to two decimal places).
  4. Determine Scale Factor: Determine the scale factor for the smaller pyramid.\newlineSince Sanjay is filling the mold 2 cm2\,\text{cm} from the top, the height of the smaller pyramid is 10 cm−2 cm=8 cm10\,\text{cm} - 2\,\text{cm} = 8\,\text{cm}. The scale factor for the height is 8 cm10 cm=0.8\frac{8\,\text{cm}}{10\,\text{cm}} = 0.8.
  5. Apply Scale Factor: Apply the scale factor to the base dimensions.\newlineThe scale factor for the volume is the cube of the scale factor for the height because volume is a three-dimensional measure. Therefore, the scale factor for the volume is 0.830.8^3.
  6. Calculate Scale Factor: Calculate the scale factor for the volume. 0.83=0.5120.8^3 = 0.512.
  7. Apply to Find Smaller Pyramid Volume: Apply the scale factor to the volume of the full-size pyramid to find the volume of the smaller pyramid.\newlineThe volume of the smaller pyramid is 0.512×333.33 cm30.512 \times 333.33\,\text{cm}^3.
  8. Perform Calculation for Smaller Pyramid: Perform the calculation for the volume of the smaller pyramid. Vsmall=0.512×333.33 cm3≈170.67 cm3V_{\text{small}} = 0.512 \times 333.33\,\text{cm}^3 \approx 170.67\,\text{cm}^3.
  9. Round Smaller Pyramid Volume: Round the volume of the smaller pyramid to the nearest cubic centimeter. Vsmall≈171 cm3V_{\text{small}} \approx 171\,\text{cm}^3 when rounded to the nearest cubic centimeter.

More problems from Pythagorean Theorem and its converse

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 7 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 8 months ago

View all (91)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant