Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Rotate the yellow dot to a location of (pi)/(2) radians. After you rotate the angle, determine the value of tan ((pi)/(2)), to the nearest hundredth.

Rotate the yellow dot to a location of π2 \frac{\pi}{2} radians. After you rotate the angle, determine the value of tan⁡π2 \tan \frac{\pi}{2} , to the nearest hundredth.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Inverses of trigonometric functions using a calculatorright chevron icon

Full solution

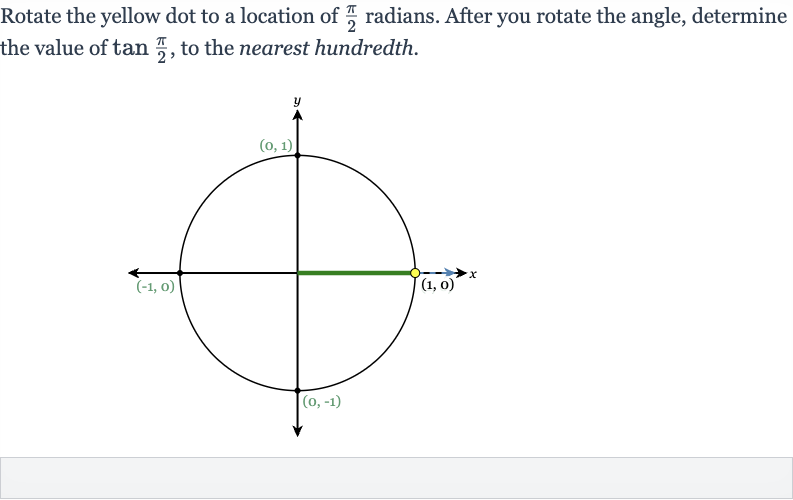
Q. Rotate the yellow dot to a location of π2 \frac{\pi}{2} radians. After you rotate the angle, determine the value of tan⁡π2 \tan \frac{\pi}{2} , to the nearest hundredth.
  1. Understand the unit circle: Understand the unit circle and the tangent function.\newlineThe tangent of an angle in the unit circle is the ratio of the y-coordinate to the x-coordinate of the point on the unit circle at that angle. However, at π2\frac{\pi}{2} radians, the point on the unit circle is directly above the origin, meaning its coordinates are (0,1)(0, 1). This makes the x-coordinate 00.
  2. Calculate tan⁡(π2)\tan\left(\frac{\pi}{2}\right): Calculate the value of tan⁡(π2)\tan\left(\frac{\pi}{2}\right).\newlineSince tan⁡(θ)=sin⁡(θ)cos⁡(θ)\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} and at θ=π2\theta = \frac{\pi}{2}, sin⁡(π2)=1\sin\left(\frac{\pi}{2}\right) = 1 and cos⁡(π2)=0\cos\left(\frac{\pi}{2}\right) = 0, we have tan⁡(π2)=10\tan\left(\frac{\pi}{2}\right) = \frac{1}{0}. This is undefined because division by zero is not possible in mathematics.
  3. Conclude tan⁡(π2)\tan\left(\frac{\pi}{2}\right): Conclude the value of tan⁡(π2)\tan\left(\frac{\pi}{2}\right).\newlineSince tan⁡(π2)\tan\left(\frac{\pi}{2}\right) is undefined, we cannot provide a numerical value to the nearest hundredth or any other precision.

More problems from Inverses of trigonometric functions using a calculator

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 1 month ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 2 months ago

View all (26)