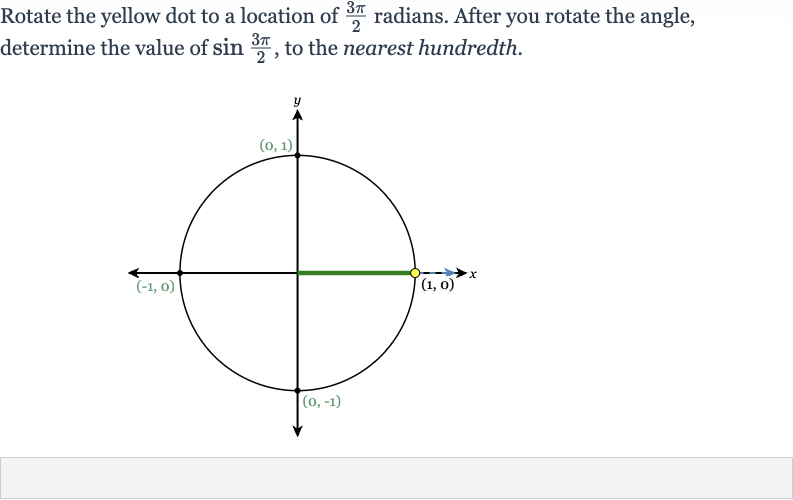
Rotate the yellow dot to a location of (3pi)/(2) radians. After you rotate the angle, determine the value of sin ((3pi)/(2)), to the nearest hundredth.

Question

Rotate the yellow dot to a location of  (3pi)/(2) radians. After you rotate the angle, determine the value of  sin ((3pi)/(2)), to the nearest hundredth.

Bytelearn · Accepted Answer

Understand unit circle and sine function: Understand the unit circle and the sine function. The sine function gives the y-coordinate of a point on the unit circle at a given angle from the positive x-axis. The unit circle is a circle with a radius of 1 centered at the origin (0,0) of the coordinate plane. The angle (3pi)/(2) radians corresponds to 270 degrees, which is directly downward from the center of the unit circle.Determine yellow dot position: Determine the position of the yellow dot after rotating (3pi)/(2) radians. When we rotate a point on the unit circle (3pi)/(2) radians, we are moving it three-quarters of the way around the circle, starting from the positive x-axis and moving counterclockwise. This places the point at the bottom of the unit circle, where the x-coordinate is 0 and the y-coordinate is -1.Calculate sin((3pi)/(2)): Calculate the value of sin((3pi)/(2)). Since the sine of an angle is the y-coordinate of the corresponding point on the unit circle, sin((3pi)/(2)) is equal to the y-coordinate of the point we found in Step 2, which is -1.Round to nearest hundredth: Round the value to the nearest hundredth. The value of sin((3pi)/(2)) is -1. Since there are no decimal places to consider, rounding to the nearest hundredth does not change the value. Therefore, the rounded value is still -1.00.

Rotate the yellow dot to a location of $\frac{3 \pi}{2}$ radians. After you rotate the angle, determine the value of $\sin \frac{3 \pi}{2}$ , to the nearest hundredth.

Full solution

More problems from Inverses of trigonometric functions using a calculator

Related topics

Rotate the yellow dot to a location of 3π2 \frac{3 \pi}{2} 23π​ radians. After you rotate the angle, determine the value of sin⁡3π2 \sin \frac{3 \pi}{2} sin23π​, to the nearest hundredth.

Rotate the yellow dot to a location of $\frac{3 \pi}{2}$ radians. After you rotate the angle, determine the value of $\sin \frac{3 \pi}{2}$ , to the nearest hundredth.