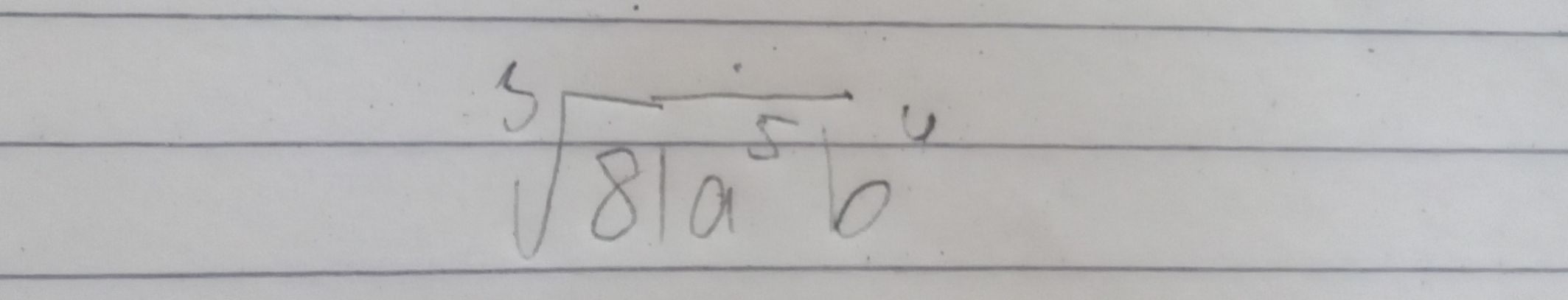AI tutor
Full solution
Q. =
- Apply cube root to factors: Apply the cube root to each factor in the expression .
- Calculate cube root of : Calculate the cube root of . Since is a perfect cube (), its cube root is simply .
- Simplify cube root of : Simplify the cube root of . We cannot simplify this further without knowing the value of ''.
- Simplify cube root of : Simplify the cube root of .
We cannot simplify this further without knowing the value of . - Combine simplified cube roots: Combine the simplified cube roots.
- Recognize cube root of : Recognize that the expression is the cube root of .