Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

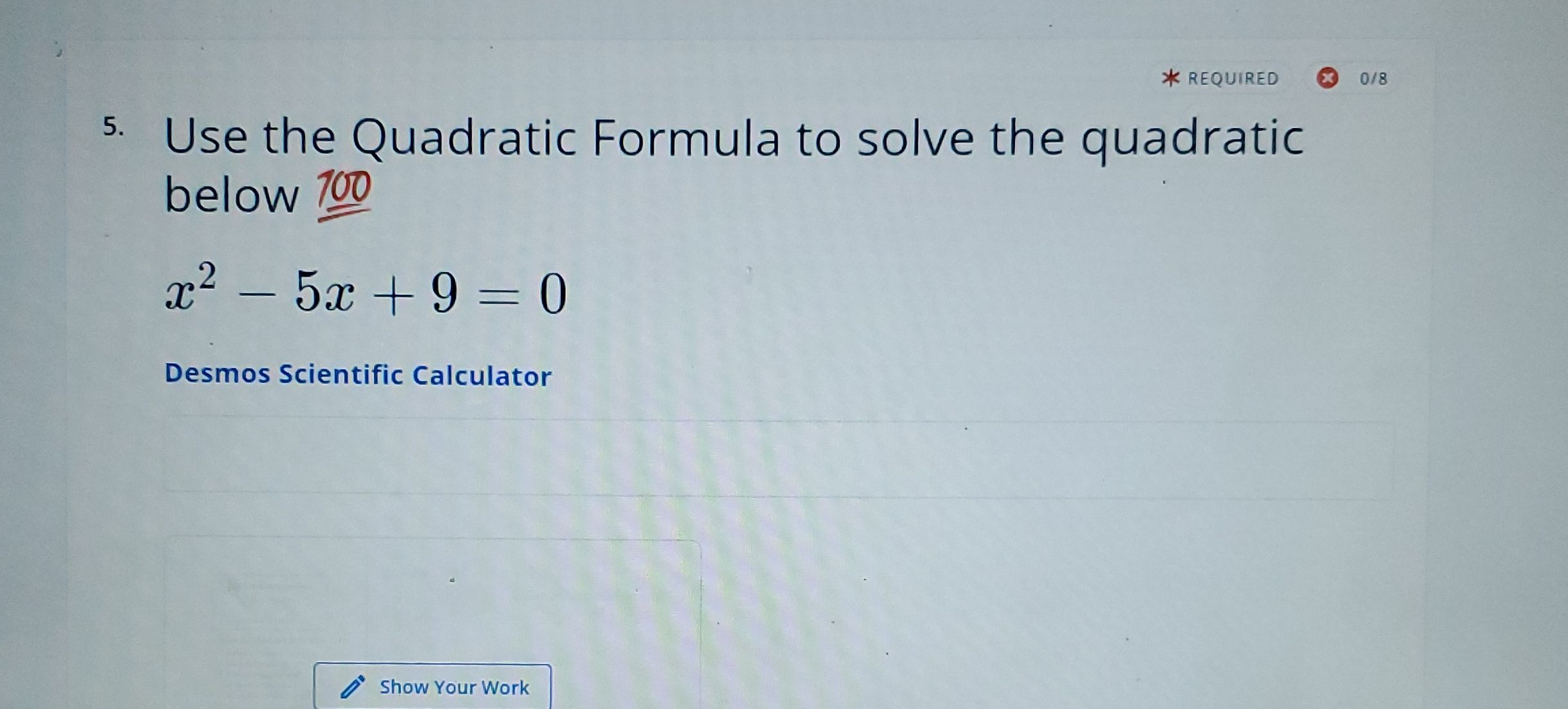
Use the Quadratic Formula to solve the quadratic below.
x^(2)-5x+9=0

Use the Quadratic Formula to solve the quadratic below. $\newline$ $x^{2}-5 x+9=0$

View step-by-step help

View step-by-step help

Factor sums and differences of cubes

Full solution

Q. Use the Quadratic Formula to solve the quadratic below.

\newline

x^{2}-5 x+9=0

Write Quadratic Formula: Write down the quadratic formula. $\newline$ The quadratic formula is used to find the solutions to a quadratic equation $ax^2 + bx + c = 0$ . The formula is: $\newline$ $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
Identify Coefficients: Identify the coefficients $a$ , $b$ , and $c$ from the quadratic equation $x^2 - 5x + 9 = 0$ . $\newline$ In this equation, $a = 1$ , $b = -5$ , and $c = 9$ .
Substitute into Formula: Substitute the coefficients into the quadratic formula. $x = \frac{-(-5) \pm \sqrt{(-5)^2 - 4(1)(9)}}{2(1)}$
Simplify Equation: Simplify the equation. $\newline$ $x = \frac{5 \pm \sqrt{25 - 36}}{2}$ $\newline$ $x = \frac{5 \pm \sqrt{-11}}{2}$
Complex Number Solutions: Since the discriminant (the value under the square root) is negative, the solutions will be complex numbers. $\newline$ $x = \frac{5 \pm \sqrt{-11}}{2}$ $\newline$ $x = \frac{5 \pm i\sqrt{11}}{2}$
Write Final Solutions: Write the final solutions. $\newline$ The solutions to the quadratic equation $x^2 - 5x + 9 = 0$ are: $\newline$ $x = \frac{5 + i\sqrt{11}}{2}$ and $x = \frac{5 - i\sqrt{11}}{2}$

More problems from Factor sums and differences of cubes

Question

Factor out the greatest common factor. If the greatest common factor is

1

, just retype the polynomial.

\newline

4x^3 - 6x^2

\newline

Posted 2 months ago

Question

x^4 + 8x^2 + 16

\newline

All factors in your answer should have integer coefficients.

\newline

Posted 2 months ago

Question

Find the binomial that completes the factorization.

\newline

t^3 + u^3 = (\underline{\hspace{1cm}}) (t^2 - tu + u^2)

Posted 2 months ago

Question

\newline

g^2 - 11g + 18

Posted 2 months ago

Question

\newline

2y^3 - y^2 + 16y - 8

\newline

\newline

Posted 2 months ago

Question

\newline

2x^8 + 7x^2

\newline

Posted 3 months ago

Question

\newline

9y^{12} + 4y^5 - y^2

\newline

Posted 3 months ago

Question

\newline

6a^4 + 3a^3 - a + 2

\newline

Posted 3 months ago

Question

\newline

4c^7 - 2c^5 + c^2 - 5

\newline

Posted 3 months ago

Question

\newline

7m^9 + 2m^6 - m^3 + 4m - 10

\newline

Posted 3 months ago