$\newline$ Given $\cot A=-\frac{5}{\sqrt{171}}$ and that angle $A$ is in Quadrant IV, find the exact value of $\sin A$ n simplest radical form using a rational denominator. $\newline$ Answer____

View step-by-step help

Home

Math Problems

Algebra 2

Find trigonometric ratios using multiple identities

Full solution

\newline

Given

\cot A=-\frac{5}{\sqrt{171}}

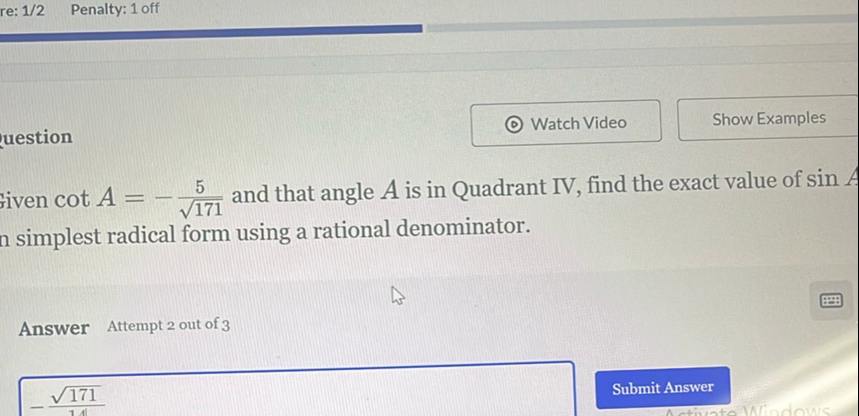
and that angle

A

is in Quadrant IV, find the exact value of

\sin A

n simplest radical form using a rational denominator.

\newline

Answer____

Use Pythagorean Identity: Use the Pythagorean identity for cotangent and sine: $\cot^2(A) + 1 = \csc^2(A)$ . Since we know $\cot A$ , we can find $\csc A$ and then $\sin A$ .
Calculate $\csc^2(A)$ : Calculate $\csc^2(A)$ using the identity: $\csc^2(A) = \cot^2(A) + 1$ . Substitute $\cot A = -\frac{5}{\sqrt{171}}$ into the identity. $\csc^2(A) = \left[-\frac{5}{\sqrt{171}}\right]^2 + 1$ $\csc^2(A) = \frac{25}{171} + 1$ $\csc^2(A) = \frac{25}{171} + \frac{171}{171}$ $\csc^2(A) = \frac{196}{171}$
Find $\csc(A)$ : Find $\csc(A)$ by taking the square root of $\csc^2(A)$ .
$\csc(A) = \sqrt{\frac{196}{171}}$
$\csc(A) = \frac{\sqrt{196}}{\sqrt{171}}$
$\csc(A) = \frac{14}{\sqrt{171}}$
Since we need a rational denominator, rationalize the denominator.
$\csc(A) = \left(\frac{14}{\sqrt{171}}\right) \cdot \left(\frac{\sqrt{171}}{\sqrt{171}}\right)$
$\csc(A) = \frac{14\sqrt{171}}{171}$
Find $\sin(A)$ : Since $\csc(A)$ is the reciprocal of $\sin(A)$ , we can find $\sin(A)$ by taking the reciprocal of $\csc(A)$ .
$\sin(A) = \frac{1}{\csc(A)}$
$\sin(A) = \frac{1}{\left(\frac{14\sqrt{171}}{171}\right)}$
$\sin(A) = \frac{171}{14\sqrt{171}}$
Simplify $\sin(A)$ : Simplify the expression for $\sin(A)$ by dividing both the numerator and the denominator by the greatest common divisor, which is $14$ .
$\sin(A) = \frac{171}{14}/\frac{\sqrt{171}\cdot 14}{14}$
$\sin(A) = \frac{171}{14}/\sqrt{171}$
$\sin(A) = \frac{171}{14} \cdot \frac{1}{\sqrt{171}}$
$\sin(A) = \frac{171}{14\cdot\sqrt{171}}$
Include negative sign: Since angle $A$ is in Quadrant IV, $\sin A$ must be negative. Therefore, we must include the negative sign in our final answer. $\newline$ $\sin(A) = -\frac{171}{14\sqrt{171}}$