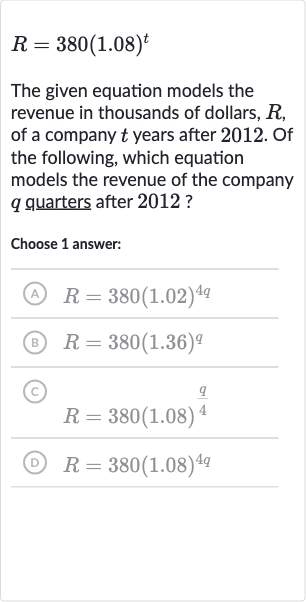
R=380(1.08)^(t) The given equation models the revenue in thousands of dollars, R, of a company t years after 2012 . Of the following, which equation models the revenue of the company q quarters after 2012 ? Choose 1 answer: (A) R=380(1.02)^(4q) (B) R=380(1.36)^(q) (C) R=380(1.08)^((q)/(4)) (D) R=380(1.08)^(4q)

Question

R=380(1.08)^(t) The given equation models the revenue in thousands of dollars,  R, of a company  t years after 2012 . Of the following, which equation models the revenue of the company  q quarters after 2012 ? Choose 1 answer: (A)  R=380(1.02)^(4q) (B)  R=380(1.36)^(q) (C)  R=380(1.08)^((q)/(4)) (D)  R=380(1.08)^(4q)

Bytelearn · Accepted Answer

Convert to Quarters: The original equation is R=380(1.08)^(t), where t is in years. We need to convert this to quarters. There are 4 quarters in a year, so we need to find the equivalent growth factor for a single quarter.Find Quarterly Growth Factor: To find the growth factor per quarter, we take the annual growth factor, which is 1.08, and take the fourth root of it because there are 4 quarters in a year. The fourth root of 1.08 can be written as (1.08)^(1/4).Calculate Quarterly Growth Factor: Now we calculate (1.08)^(1/4) to find the quarterly growth factor. This can be done using a calculator or approximating the value.Approximate Quarterly Growth Factor: Using a calculator, we find that (1.08)^(1/4) is approximately 1.0198, which can be rounded to 1.02 for simplicity. This is the growth factor per quarter.Express Revenue in Quarters: Now we need to express the revenue R in terms of q quarters. Since the growth factor per quarter is 1.02, and there are q quarters, the equation becomes R=380(1.02)^(q).Adjust for Quarterly Growth: However, we need to account for the fact that the growth happens every quarter, not annually. Therefore, we need to raise the growth factor to the power of 4q to represent q quarters. The correct equation is R=380(1.02)^(4q).

Full solution

More problems from Solve quadratic equations: word problems

Related topics