Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

What is the image point of (-6,-1) after the transformation R_(180) o r_(y) = - x ?

What is the image point of (−6,−1) (-6,-1) after the transformation R180 R_{180} o ry=−xr_{y} = - x ?

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find trigonometric functions using a calculatorright chevron icon

Full solution

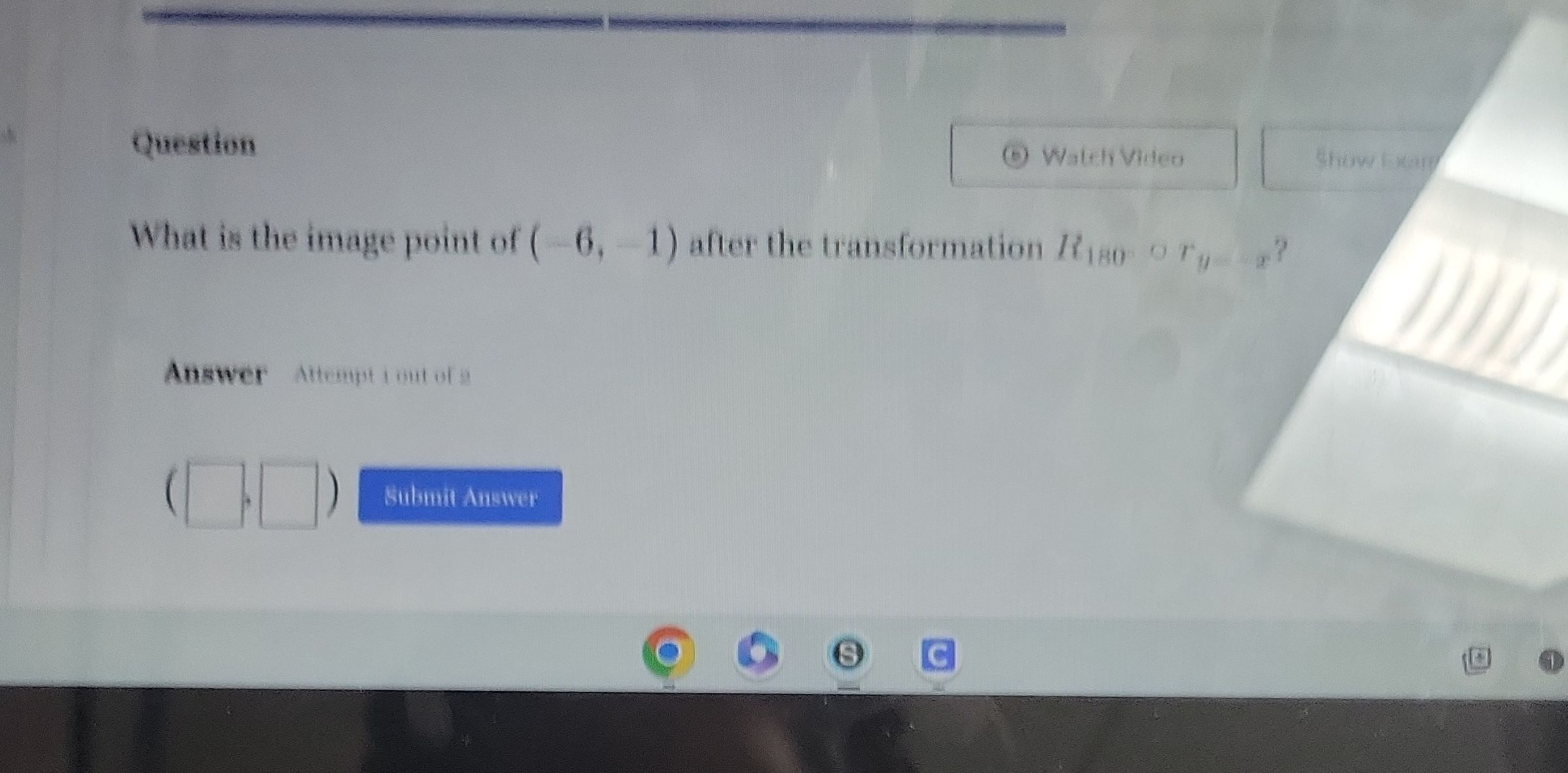
Q. What is the image point of (−6,−1) (-6,-1) after the transformation R180 R_{180} o ry=−xr_{y} = - x ?
  1. Perform Rotation: The transformation R180quadr11x2R_{180}\text{quadr}_{11}x_{2} seems to be a combination of a rotation by 180180 degrees and a translation. However, the notation is not standard. Assuming ＂R180R_{180}＂ means rotation by 180180 degrees around the origin and ＂quadr11x2\text{quadr}_{11}x_{2}＂ means translation by a vector, we need to clarify the translation vector. For the purpose of this solution, I will assume that the translation vector is (11,2)(11, 2). First, we will perform the rotation of the point (6,1)(6,1) by 180180 degrees around the origin.
  2. Calculate New Coordinates: To rotate a point (x,y)(x, y) by 180180 degrees around the origin, the new coordinates become (−x,−y)(-x, -y). So, the image of the point (6,1)(6,1) after rotation by 180180 degrees is (−6,−1)(-6, -1).
  3. Perform Translation: Next, we perform the translation using the vector (11,2)(11, 2). To translate a point (x,y)(x, y) by a vector (a,b)(a, b), we add the vector components to the point's coordinates, resulting in a new point (x+a,y+b)(x+a, y+b). Therefore, we add (11,2)(11, 2) to the point (−6,−1)(-6, -1).
  4. Final Coordinates: Adding the translation vector (11,2)(11, 2) to the rotated point (−6,−1)(-6, -1) gives us the new coordinates: (−6+11,−1+2)=(5,1)(-6 + 11, -1 + 2) = (5, 1).

More problems from Find trigonometric functions using a calculator

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 7 months ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 7 months ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 7 months ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 7 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 9 months ago

View all (217)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant