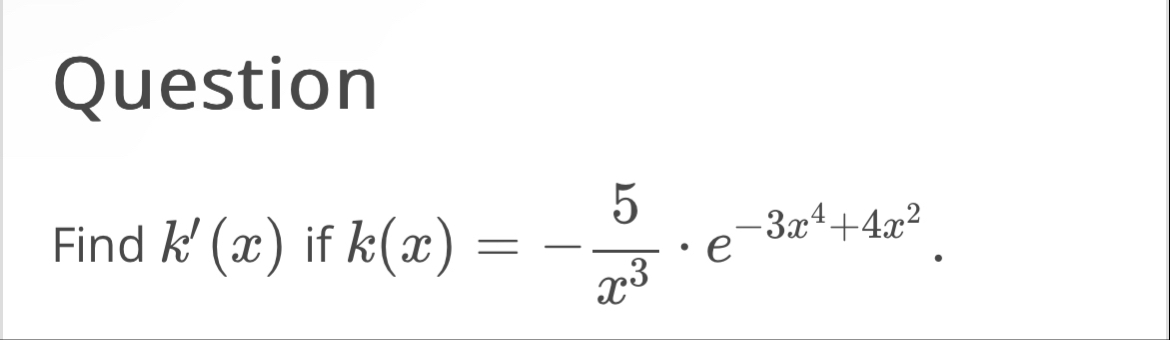Find k^(')(x) if k(x)=-(5)/(x^(3))*e^(-3x^(4)+4x^(2)).

Question

Bytelearn · Accepted Answer

Identify Functions: We need to find the derivative of the function k(x) = -(5/x^3)*e^(-3x^4 + 4x^2). This requires the use of the product rule and the chain rule, as we have a product of two functions: -5/x^3 and e^(-3x^4 + 4x^2).Find u'(x): First, let's identify the two functions we will be differentiating. Let u(x) = -5/x^3 and v(x) = e^(-3x^4 + 4x^2). We will find the derivatives u'(x) and v'(x) separately.Find v'(x): To find u'(x), we differentiate -5/x^3 with respect to x. This is a power rule problem, and the derivative of x^n is n*x^(n-1). So, u'(x) = -5 * (-3) * x^(-3 - 1) = 15x^(-4).Apply Chain Rule to v(x): Now, we need to find v'(x). Since v(x) is an exponential function with a composite function in the exponent, we will use the chain rule. The derivative of e^f(x) is e^f(x)*f'(x), where f(x) = -3x^4 + 4x^2.Apply Chain Rule to v'(x): We find the derivative of f(x) = -3x^4 + 4x^2. Using the power rule, f'(x) = -3 * 4x^3 + 4 * 2x = -12x^3 + 8x.Apply Product Rule to k'(x): Now we apply the chain rule to find v'(x). v'(x) = e^(-3x^4 + 4x^2) * (-12x^3 + 8x).Substitute Derivatives: With u'(x) and v'(x) found, we can now apply the product rule to find k'(x). The product rule states that (uv)' = u'v + uv'. So, k'(x) = u'(x)v(x) + u(x)v'(x).Simplify Expression: Substitute the derivatives and original functions into the product rule formula. k'(x) = (15x^(-4)) * (e^(-3x^4 + 4x^2)) + (-5/x^3) * (e^(-3x^4 + 4x^2) * (-12x^3 + 8x)).Further Simplify Expression: Simplify the expression by combining like terms and factoring out common factors if possible. k'(x) = 15x^(-4)e^(-3x^4 + 4x^2) - (5/x^3)e^(-3x^4 + 4x^2)(-12x^3 + 8x).Combine Terms: Further simplify the expression by multiplying through the parentheses. k'(x) = 15x^(-4)e^(-3x^4 + 4x^2) + (5/x^3)e^(-3x^4 + 4x^2)(12x^3) - (5/x^3)e^(-3x^4 + 4x^2)(8x).Final Derivative Form: Combine the terms with common factors. k'(x) = 15x^(-4)e^(-3x^4 + 4x^2) + 60e^(-3x^4 + 4x^2) - 40x^(-2)e^(-3x^4 + 4x^2).The final simplified form of the derivative is k'(x) = e^(-3x^4 + 4x^2)(15x^(-4) + 60 - 40x^(-2)).

Find $k^{\prime}(x)$ if $k(x)=-\frac{5}{x^{3}} \cdot e^{-3 x^{4}+4 x^{2}}$ .

Full solution

More problems from Multiplication with rational exponents

Related topics

Find k′(x) k^{\prime}(x) k′(x) if k(x)=−5x3⋅e−3x4+4x2 k(x)=-\frac{5}{x^{3}} \cdot e^{-3 x^{4}+4 x^{2}} k(x)=−x35​⋅e−3x4+4x2.

Find $k^{\prime}(x)$ if $k(x)=-\frac{5}{x^{3}} \cdot e^{-3 x^{4}+4 x^{2}}$ .