Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

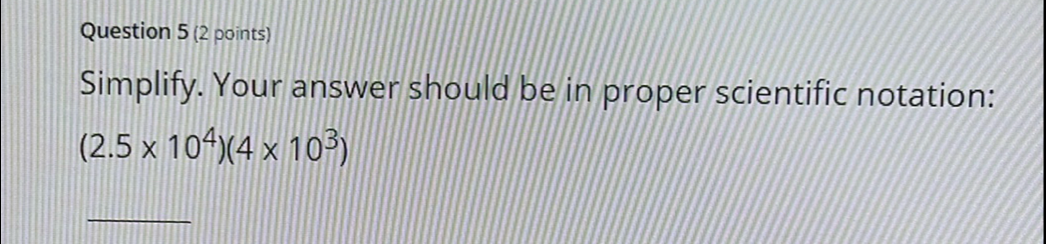
Simplify. Your answer should be in proper scientific notation: (2.5 ×10^(4))(4×10^(3))

Simplify. Your answer should be in proper scientific notation:\newline(2.5×104)(4×103) \left(2.5 \times 10^{4}\right)\left(4 \times 10^{3}\right)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Write a quadratic function from its x-intercepts and another pointright chevron icon

Full solution

Q. Simplify. Your answer should be in proper scientific notation:\newline(2.5×104)(4×103) \left(2.5 \times 10^{4}\right)\left(4 \times 10^{3}\right)
  1. Question Prompt: Question prompt: What is the product of (2.5×104)(2.5 \times 10^4) and (4×103)(4 \times 10^3) in proper scientific notation?\newlineTo multiply two numbers in scientific notation, we multiply their coefficients and add the exponents of 1010.\newlineCalculation: (2.5×104)×(4×103)=(2.5×4)×(104×103)(2.5 \times 10^4) \times (4 \times 10^3) = (2.5 \times 4) \times (10^4 \times 10^3)
  2. Calculation: Now we calculate the product of the coefficients and the sum of the exponents separately.\newlineCalculation for coefficients: 2.5×4=102.5 \times 4 = 10\newlineCalculation for exponents: 104×103=104+3=10710^4 \times 10^3 = 10^{4+3} = 10^7
  3. Calculation for Coefficients: Combine the results to get the product in scientific notation.\newlineCalculation: 10×10710 \times 10^7\newlineHowever, the coefficient 1010 is not between 11 and 9.999.99, which is required for proper scientific notation.
  4. Calculation for Exponents: To convert the coefficient to a number between 11 and 9.999.99, we can express 1010 as 1.0×1011.0 \times 10^1.\newlineCalculation: 10×107=(1.0×101)×107=1.0×101+7=1.0×10810 \times 10^7 = (1.0 \times 10^1) \times 10^7 = 1.0 \times 10^{1+7} = 1.0 \times 10^8\newlineNow the number is in proper scientific notation.

More problems from Write a quadratic function from its x-intercepts and another point

Question
Solve by completing the square.\newlinem2−10m−29=0m^2 - 10m - 29 = 0\newlineWrite your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.\newline`m` = ____ or `m` = _____
Get tutor helpright-arrow

Posted 8 months ago

Question
Find g(x) g(x) , where g(x) g(x) is the translation 5 5 units up of f(x)=x2 f(x)=x^2 .\newlineWrite your answer in the form a(x–h)2+k a(x–h)^2+k , where a a , h h , and k k are integers.\newlineg(x)= g(x)= ____
Get tutor helpright-arrow

Posted 7 months ago

Question
What is the range of this quadratic function?\newliney=x2−4x+4y = x^2 - 4x + 4\newlineChoices:\newline{y∣y≥2}\left\{y \mid y \geq 2\right\}\newline{y∣y≤0}\left\{y \mid y \leq 0\right\}\newline{y∣y≥0}\left\{y \mid y \geq 0\right\}\newlineall real numbers\text{all real numbers}
Get tutor helpright-arrow

Posted 5 months ago

Question
Write the equation of the parabola that passes through the points (1,0)(1,0), (2,0)(2,0), and (3,–16)(3,\text{–}16). Write your answer in the form y=a(x–p)(x–q)y = a(x – p)(x – q), where aa, pp, and qq are integers, decimals, or simplified fractions.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic.\newlinef2+8f+_____f^2 + 8f + \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Solve for h h .\newlineh2+39h=0 h^2 + 39h = 0 \newline\newlineWrite each solution as an integer, proper fraction, or improper fraction in simplest form. If there are multiple solutions, separate them with commas.\newlineh= h = ____\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Write a quadratic function with zeros −9-9 and −7-7.\newlineWrite your answer using the variable xx and in standard form with a leading coefficient of 11.\newlinef(x)=_____f(x) = \_\_\_\_\_
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the equation of the axis of symmetry for the parabola y=x2y = x^2. \newlineSimplify any numbers and write them as proper fractions, improper fractions, or integers.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 4 months ago

Question
Find g(x)g(x), where g(x)g(x) is the translation 88 units up of f(x)=x2f(x) = x^2.\newlineWrite your answer in the form a(x–h)2+ka(x – h)^2 + k, where aa, hh, and kk are integers.\newlineg(x)=g(x) = ______\newline
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve for xx.\newlinex2=1x^2 = 1\newline\newlineWrite your answer in simplified, rationalized form.\newlinex=x = ______ or x=x = ______\newline
Get tutor helpright-arrow

Posted 5 months ago

View all (106)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant